Méthodes de base en métrologie : les méthodes de pesée

Contrairement à une idée trop répandue, la métrologie ne se limite pas à calculer des incertitudes. De façon générale, il est indispensable lorsque l'on doit faire une mesure de chercher à réduire, voir éliminer, les erreurs qui peuvent survenir. Cette phase essentielle de réduction des erreurs doit intervenir au moment même de la conception de la mesure. Le meilleur moyen d'y parvenir est encore d'avoir en permanence à l'esprit un certain nombre de méthodes de base que l'on devrait apprendre dans tout bon cours de métrologie générale. Parmi ces méthodes, l'on peut citer : les méthodes directes ou par inversion ou par substitution, la méthode du retournement, la méthode des séries fermées, la méthode des répétitions, la méthodes des coïncidences… On pourrait même ajouter à ces méthodes souvent anciennes de nouvelles pistes telles que la surabondance des mesures (pour réduire les incertitudes à l'aide de capteurs de base commerciaux, déceler des anomalies lors des mesures, etc.) qui est rendue possible aujourd'hui grâce à la baisse des coût des capteurs et aux progrès de l'informatique. L'enseignement de ces méthodes devrait figurer dans toutes les formations scientifiques et techniques : il n'est en effet pas rare de constater que beaucoup de bancs de contrôle et d'essais dans les entreprises pourraient offrir de bien meilleures exactitudes (et sans surcoût !) si l'on s'était simplement inspiré des méthodes de base issues de la métrologie générale. L'objectif des lignes qui suivent n'est évidement pas de faire un inventaire exhaustif de ces méthodes de mesure, mais simplement de présenter les méthodes directes par inversion et par substitution au travers des différentes méthodes de pesée (directe, de Borda ou de Gauss). Cette présentation permet de souligner l'importance du bon choix de la méthode de mesure sur l'incertitude du résultat final, c'est à dire d'influer sur la capabilité de l'équipement de contrôle dans le cadre du process de mesure.

1. La pesée simple

On équilibre directement une masse m₁ par une masse m₂ comme indiqué sur la figure 1.

Fig. 1. - La pesée simple.

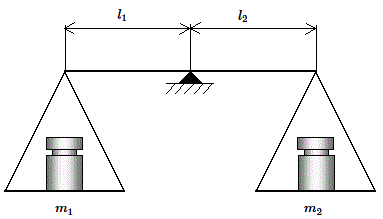
A l'équilibre, la somme des torseurs étant égale au torseur nul, on obtient notamment :

\( m_{1} \cdot g_{1} \cdot l_{1} = m_{2} \cdot g_{2} \cdot l_{2} \) ,

(1)

en supposant l'accélération de la pesanteur uniforme (g₁ = g₂) on a :

\( \begin{eqnarray} m_{1} = \dfrac { m_{2} \cdot l_{2}} { l_{1}} \end{eqnarray} \) .

(2)

Exprimons à présent u (m₁) l'incertitude type sur la masse m₁. A partir de l'équation (2) et de la loi de propagation des variances on obtient l'expression suivante :

\( \begin{eqnarray} u(m_{1}) = \sqrt{ \left(\dfrac{l_{2}}{l_{1}}\right)^{2} \cdot u^{2}(m_{2}) + \left( \dfrac{m_{2}}{l_{1}} \right)^{2} \cdot u^{2}(l_{2}) + \left( \dfrac{ m_{2} \cdot l_{2} }{ l_{1}^{2} } \right)^{2} \cdot u^{2}(l_{1}) } \end{eqnarray} \) ,

(3)

avec :

•	u (m₂)	: l'incertitude type sur m₂ ;
•	u (l₁)	: l'incertitude type sur l₁ ;
•	u (l₂)	: l'incertitude type sur l₂.

De façon générale, les valeurs de l₁ et l₂ sont difficiles à connaître avec de faibles incertitudes. Pour cette raison, la méthode de la pesée simple n'est pas conseillée. Il vaut mieux employer d'autres méthodes de pesée telles que la double pesée de Borda (mesure par substitution) ou la double pesée de Gauss (mesure par inversion).

2. La double pesée de Borda

Cette pesée comporte deux étapes :

1^ère étape on place m₁ sur le plateau que l'on équilibre avec une tare T comme repéré sur la figure 2.

Fig. 2. - La double pesée de Borda - première étape.

2^e étape on retire m₁ du plateau et on équilibre la tare T avec la masse m₂ comme indiqué sur la figure 3.

Fig. 3. - La double pesée de Borda - deuxième étape.

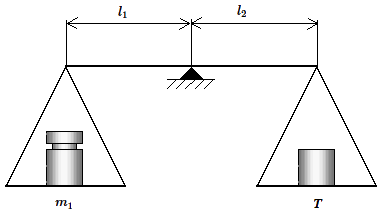
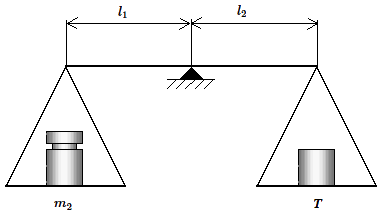
Si l'on suppose que l'équilibre est le même on a donc dans une première approximation :

m₁ = m₂ ,

(4)

ce qui conduit à :

u (m₁) = u (m₂) .

(5)

Cette méthode de pesée permet donc de s'affranchir des incertitudes sur l₁ et l₂ contrairement à la pesée simple.

3. La double pesée de Gauss

Comme la double pesée de Borda, cette méthode de pesée comporte deux étapes :

1^ère étape on place m₁ sur le premier plateau que l'on équilibre avec une masse m₂ comme repéré sur la figure 4.

Fig. 4. - La double pesée de Gauss - première étape.

2^e étape on place m₁ sur le deuxième plateau que l'on équilibre avec m₃ comme indiqué sur la figure 5.

Fig. 5. - La double pesée de Gauss - deuxième étape.

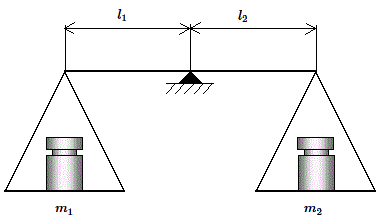
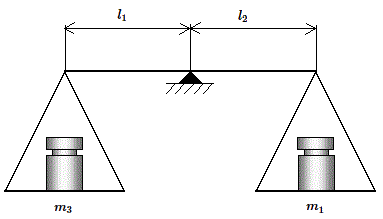
A l'issue de la première étape l'équilibre s'écrit :

\( m_{1} \cdot g_{1} \cdot l_{1} = m_{2} \cdot g_{2} \cdot l_{2} \) .

(6)

A l'issue de la deuxième étape l'équilibre s'écrit :

\( m_{1} \cdot g_{2} \cdot l_{2} = m_{3} \cdot g_{1} \cdot l_{1} \) .

(7)

En multipliant (6) et (7) on obtient après simplification :

\( \begin{eqnarray} m_{1} = \sqrt{ m_{2} \cdot m_{3}} \end{eqnarray} \)

(8)

L'application de la loi de propagation des variances à cette expression conduit à :

\( \begin{eqnarray} u(m_{1}) = \sqrt{ \left( \dfrac{ m_{3} }{ 2 \times \sqrt{ m_{2} \cdot m_{3} } } \right)^{2} \cdot u^{2}(m_{2}) + \left( \dfrac{ m_{2} }{ 2 \times \sqrt{ m_{2} \cdot m_{3} } } \right)^{2} \cdot u^{2}(m_{3}) } \end{eqnarray} \) .

(9)

En conclusion, comme pour la méthode par substitution, la méthode par inversion permet de s'affranchir des incertitudes sur l₁ et l₂ contrairement à la méthode directe.