La masse volumique de l'eau a une importance particulière en métrologie. Celle-ci est en effet utilisée comme référence dans la majorité des cas pour la détermination de la masse volumique et des volumes des solides. La valeur de la masse volumique de l'eau doit alors être déterminée au moyen d'une formule en fonction de la pression et de la température du fluide.

1. Formules disponibles

  Un certain nombre de normes, de documents utilisés dans le cadre de la métrologie légale fournissent des abaques ou des formules polynomiales simplifiées pour calculer la masse volumique de l'eau (e.g. [1]). Généralement ces abaques et formules ont été élaborées à partir de données de mesure datant de la première moitié du XX^e siècle et ne sont pas assorties d'incertitudes, i.e. une exactitude non maîtrisée et une traçabilité non assurée. A partir des années 1990 plusieurs expériences permettant la mesure de la masse volumique de l'eau ont été effectuées par plusieurs laboratoires de métrologie à l'échelle internationale [2, 3, 4, 5]. Ces travaux ont servi de base pour élaborer deux formules qui permettent aujourd'hui de calculer la masse volumique de l'eau avec une incertitude connue. L'une a été diffusée sous couvert du Comité international des poids et mesures (CIPM) et l'autre de l'International Association for the Properties of Water and Steam (IAPWS).

Les deux formules s'appliquent à de l'eau dite VSMOW (Vienna Standard Mean Ocean Water) qui est un matériau de référence défini par l'AIEA en 1968. Il s'agit d'une eau pure, ne contenant pas d'air, avec la composition isotopique suivante :
- 0,000 155 76 mole de \( ^{2}\text{H} \) pour une mole de \( ^{1}\text{H} \) ;
- 0,000 379 9 mole de \( ^{17}\text{O} \) pour une mole de \( ^{16}\text{O} \) ;
- 0,002 005 2 mole de \( ^{18}\text{O} \) pour une mole de \( ^{16}\text{O} \).

2. Formule du CIPM

2.1. Cas de l'eau VSMOW

En 2001, le CIPM a diffusé une formule permettant de calculer la masse volumique de l'eau entre 0 °C et 40 °C [6]. La masse volumique de l'eau est modélisée en utilisant la formule de Thiesen (1) qui a été proposée au début du vingtième siècle :

dans laquelle t est la température de l'eau en degrés Celsius et a₁, …, a₅ cinq coefficients. Une nouvelle détermination de ces coefficients a été effectuée plus récemment dans [6] en considérant les résultats de quatre expériences :

• les mesures de masse volumique relative de Takenaka et Masui [2] (mesure de la variation de volume de l'eau entre 0 °C et 85 °C avec un dilatomètre en quartz) ;
• les mesures de masse volumique relative de Watanabe [3] (mesure de la poussée d'Archimède sur un plongeur en quartz entre 0 °C et 44 °C) ;
• les mesures de masse volumique de Patterson et Morris [4] (mesure de la poussée d'Archimède sur une sphère de masse et de valeurs connues immergée dans l'eau entre 1 °C et 40 °C) ;
• les mesures de masse volumique de Masui, Fujii et Takenaka [5] (mesure de la poussée d'Archimède sur une sphère en quartz de masse et de volumes connues immergée dans l'eau à 16 °C).

Les valeurs qui suivent ont été déterminées par la méthode du chi-carré :

  L'incertitude élargie (k = 2) sur la masse volumique calculée à partir de (1) et (2) a été modélisée dans [6] par le polynôme du 4^e degré suivant :

avec

2.2. Corrections additionnelles pour l'eau « usuelle »

Ces corrections sont fournies avec la formule du CIPM [6].

2.2.1. Correction due à la pression

La formule donnant la masse volumique de l'eau a été calculée pour une pression atmosphérique de 101 325 Pa. L'eau étant compressible, il est nécessaire de corriger la valeur de la masse volumique calculée pour des pressions différentes. On peut utiliser la facteur multiplicatif donné par la formule (5) :

avec t la température de l'eau, p la pression atmosphérique et les coefficients (6) suivants :

Ceci étant la plage de validité en pression et l'incertitude associées à cette correction ne sont pas documentées.

2.2.2. Correction due à la présence d'air dissout

  La formule donnant la masse volumique de l'eau a été calculée en supposant qu'il n'y avait pas d'air dissout dans l'eau. La correction à ajouter pour déterminer la masse volumique de l'eau saturée d'air s'obtient pour une température t comprise entre 0 °C et 25 °C en utilisant la formule (7) :

avec

Remarque : dans la pratique l'eau n'est pas saturée, mais la connaissance de l'erreur maximale permet d'insérer une contribution de l'incertitude calculée par une loi uniforme.

2.2.3. Correction due à la composition isotopique

  La formule donnant la masse volumique de l'eau concerne l'eau « VSMOW ». Cette eau diffère par sa composition isotopique de l'eau du robinet. Pour de l'eau du robinet, il est courant de remplacer dans les coefficients (2) :

2.3. Limitation des corrections additionnelles

  L'inconvénient de ces correction additionnelles est que leur domaine de définition et par conséquent leur incertitude ne sont pas définis, ce qui fait perdre l'intérêt de l'exactitude de la formule du CIPM. En particulier pour travailler sur des plages de température et de pression plus étendues, il faut alors utiliser la formule de l'IAPWS.

3. Formule de l'IAPWS

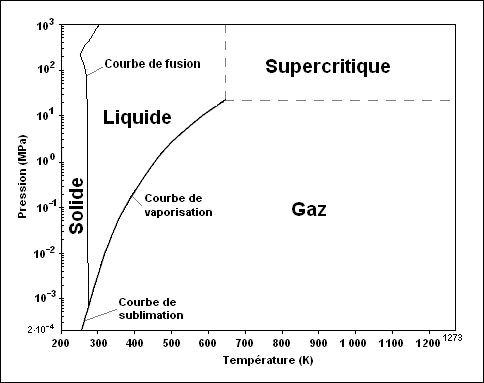
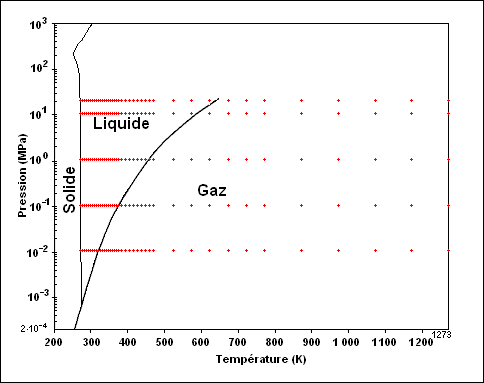
  En 1995, l'IAPWS a élaboré une formule, qui sera appelée IAPWS-95 par la suite, permettant de déterminer la fonction d'énergie libre de Helmholtz. Cette formule est trop complexe pour être détaillée dans ces lignes. Elle est fournie intégralement dans la référence [7]. Moyennant certaines opérations algébriques, elle permet d'extraire plusieurs paramètres de l'eau : pression, énergie interne, entropie, enthalpie, capacités calorifiques, vitesse du son, masse volumique... La formule déterminée par l'IAPWS est définie entre la courbe de fusion de l'eau jusqu'à une température de 1 273 K et une pression de 1 GPa (fig. 1).

  La formule IAPWS-95 est fournie avec des incertitudes sous la forme d'un graphique (fig. 2). Ceci étant, celles-ci ne sont pas calculées par la méthode du GUM [8]. En réalité, les valeurs indiquées par l'IAPWS découlent des écarts constatés par comparaisons entre la formule et les données expérimentales qui sont traçables à des étalons nationaux. En d'autres termes, les intervalles fournis par l'IAPWS garantissent la traçabilité, ce qui est la fonction première d'une incertitude, mais ne sont pas calculés par des méthodes statistiques. Les intervalles étant choisis pour prendre en compte les écarts maximums, on peut considérer qu'ils correspondent à des incertitudes avec un facteur d'élargissement égal à 2. La formule IAPWS-95 ne doit pas être confondue avec la formulation industrielle de l'IAPWS souvent désignée IAPWS-IF97 [9]. Cette seconde formulation contient des formules plus simples que l'IAPWS-95 définies sur certaines zones de la courbe de phase mais sont moins exactes que l'IAPWS-95. En d'autres termes, l'IAPWS-IF97 n'est pas adaptée à un usage métrologique visant les meilleures incertitudes.

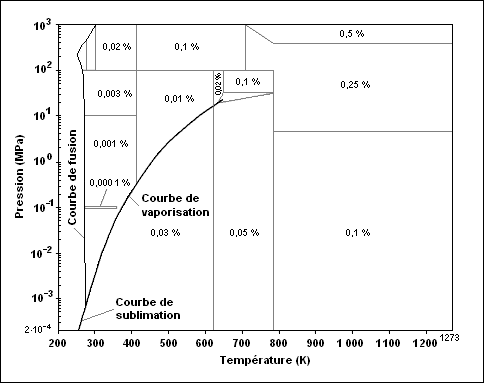
Les valeurs d'incertitudes indiquées sur la figure 2 correspondent à l'incertitude de modélisation. Pour obtenir l'incertitude sur la masse volumique, il faut également prendre en compte les incertitudes sur la température et sur la pression. Le modèle de la mesure s'écrit :

En appliquant la loi de propagation des variances à la formule (9), l'incertitude vaut :

Remarque : dans la pratique les valeurs des dérivées de la masse volumique peuvent être estimées en calculant des taux de variation.

4. Compatibilité des formules

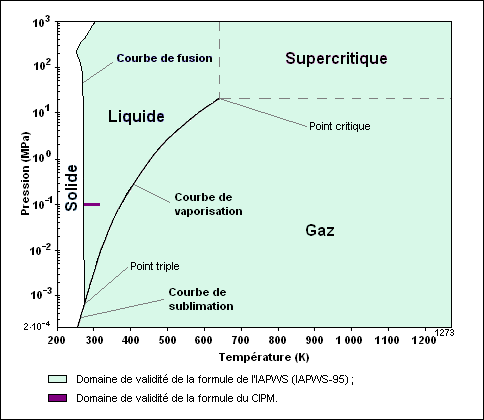
  Les domaines de définition des deux formules sont rappelés sur la figure 3.

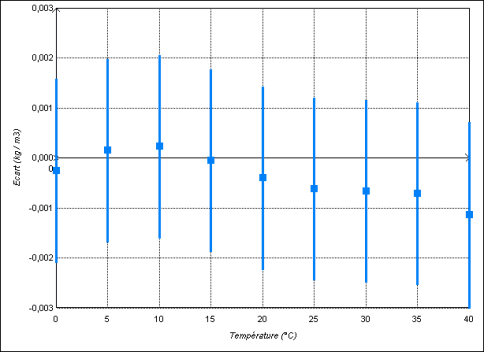
La figure 4 représente l'écart entre les masses volumiques calculées par les deux formules sur leur domaine commun (entre 0 °C et 40 °C, à 101 325 Pa) et montre qu'elles sont en accord aux incertitudes près.

5. Choix des formules

  Une recommandation commune entre le CIPM et l'IAPWS a été élaborée concernant le choix des formules [10, 11]. Ses principales conclusions sont résumées dans les lignes qui suivent.

1. Entre 0 °C et 40 °C pour des pressions proches de la pression atmosphérique (101 325 Pa), il faut utiliser la formule du CIPM. Cette formule offre la meilleure incertitude. Elle ne doit pas être extrapolée en dehors de son domaine de définition.
2. Les masses volumiques calculées par la formule du CIPM et la formule IAPWS-95 sont en accord aux incertitudes près, sur le domaine de définition commun qui correspond au domaine de définition de la formule du CIPM.
3. Dans le cas ou il est nécessaire de calculer des masses volumiques sur un domaine dans lequel la formule du CIPM est partiellement applicable, il est préférable d'utiliser la formule IAPWS-95 pour éviter les discontinuités.

6. Le logiciel DensiCal

Le logiciel DensiCal permet de calculer la masse volumique de l'eau VSMOW avec :

• la formule du CIPM entre 0 °C et 40 °C, pour une pression de 101 325 Pa ;
• la formule IAPWS-95 entre la courbe de fusion (approximativement 273,15 K, i.e. 0 °C) et 1 273,15 K, i.e. 1 000 °C), pour des pressions comprises entre 611,211 Pa et 20 MPa (i.e. entre 0,006 11 bar et 200 bar).

6.1. Méthodes de calcul employées

Concernant la formule du CIPM, les calculs sont effectués à partir de (1) et (2). Concernant l'IAPWS-95, les calculs de masse volumique sont effectués en utilisant la formule permettant de calculer la pression à partir de la masse volumique et de la température ([7], tableau 3). En conservant les notations de [7], cette formule s'écrit :

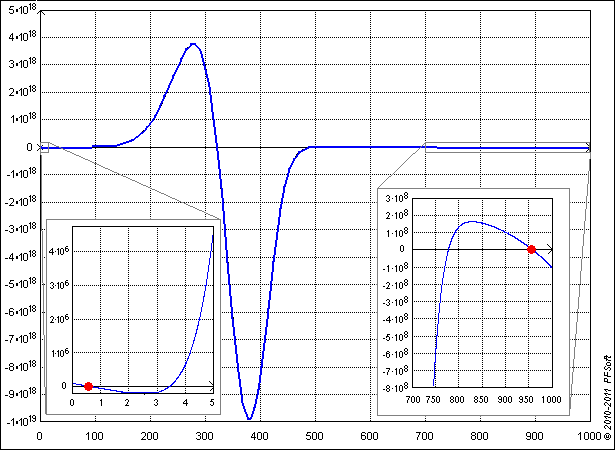
Cette formule ne permet pas d'exprimer sous forme littérale la masse volumique en fonction de la pression et de la température. La méthode employée consiste donc pour une température T et une pression p données à rechercher les racines annulant la fonction :

La discontinuité de la masse volumique lors des changements d'états correspond à un changement de racines : la figure 5 présente cette fonction et les racines correspondant à la masse volumique de la phase gazeuse et de la phase liquide pour des conditions de pression et de température proches de la courbe de vaporisation.

6.2. Fonctions de base

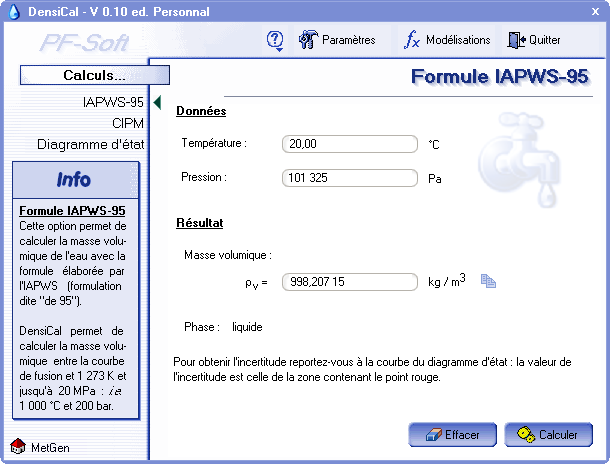
6.2.1. Calcul avec la formule IAPWS-95

  Cette option est disponible en cliquant sur « IAPWS-95 » situé dans le bandeau à gauche de l'écran (fig. 1). Les données à saisir sont la température et la pression. En cliquant sur le bouton « calculer », la masse volumique est alors affichée.

  Concernant l'incertitude sur la valeur de la masse volumique, l'IAPWS ne fournie pas de formule mais un diagramme d'état de l'eau découpé en zones sur lesquelles sont indiqués des pourcentages correspondants aux incertitudes élargies. Pour obtenir l'incertitude sur DensiCal, il faut cliquer sur « diagramme d'état » sur le bandeau gauche de l'écran, relever le pourcentage situé sous le point rouge et l'appliquer à la valeur de la masse volumique (fig. 7).

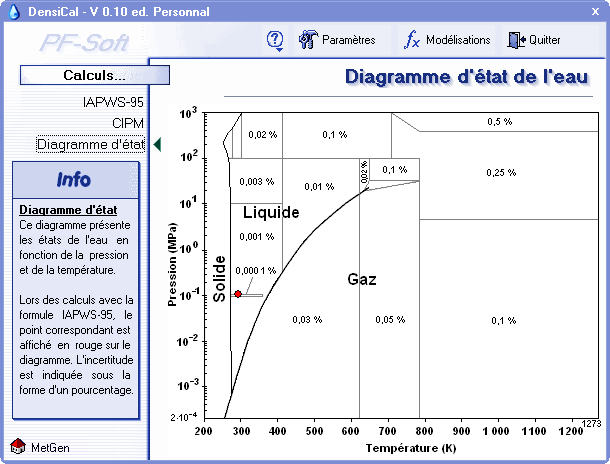
  Lorsque que les conditions de pression et de température sont à la limite des courbes de fusion ou de vaporisation, une alerte est indiqué. Dans le cas de la courbe de fusion, les masses volumiques correspondant à la vapeur et à la la phase liquide sont fournies. Les courbes de fusion et de vaporisation sont calculées par des modèles approchés. Pour tenir compte des approximations, l'alerte est déclenchée sur une plage de valeurs de température autour des courbes de fusion et de vaporisation. L'étendue de ces plages de température peut être modifiée au moyens des seuils d'alerte accessibles dans l'onglet « divers » de la fenêtre de paramétrage.

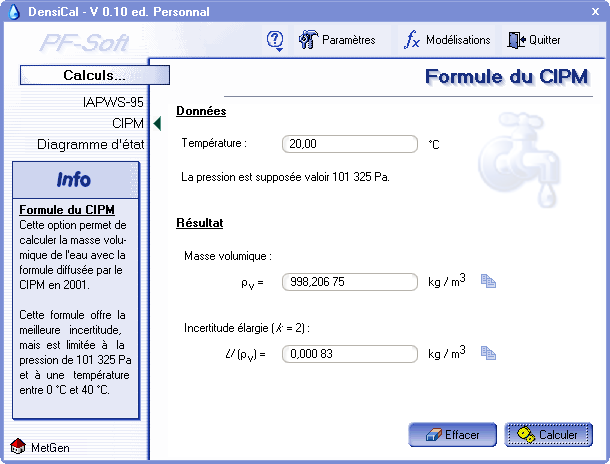
6.2.2. Calcul avec la formule du CIPM

  Cette option est disponible en cliquant sur « CIPM » situé dans le bandeau à gauche de l'écran (fig. 8). Cette formule s'applique pour une pression de 101 325 Pa. La donnée d'entrée restante à saisir est donc la température. En cliquant sur le bouton « calculer », la masse volumique est alors affichée.

Une alerte est indiquée lorsque que les conditions de pression et de température sont à la limite de la courbe de fusion. La courbe de fusion est calculée par un modèle approché. Pour tenir compte des approximations, l'alerte est déclenchée sur une plage de valeurs de température autour de la courbe de fusion. L'étendue de cette plage de température peut être modifiée au moyens du seuil d'alerte de fusion accessible dans l'onglet « divers » de la fenêtre de paramétrage.

6.2.3. Modélisations des courbes de fusion et de vaporisation

  Cette option est accessible en cliquant sur le bouton « modélisations » et fait apparaître l'écran reproduit sur la figure 9. Elle permet de calculer :

• la pression de vaporisation à une température donnée à partir de la modélisation décrite dans [9] ;
• la température de vaporisation à une pression donnée à partir de la modélisation décrite dans [9] ;
• la pression de fusion à une température donnée à partir de la modélisation décrite dans [12] ;
• la température de fusion à une pression donnée à partir de la modélisation décrite dans [12].

6.3. Validation

6.3.1. Masse volumique

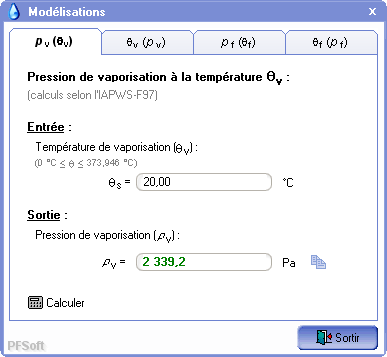
  La masse volumique calculée au moyen de DensiCal a été comparée à 210 valeurs de masse volumiques calculées par le NIST [13]. Ces valeurs correspondent à une plage de température allant de 0 °C à 1 000 °C et une plage de pression allant de 0,01 MPa (0,1 bar) à 20 MPa (200 bar) représentées sur la figure 10. En conservant les résolutions du NIST, il n'y a pas d'écart entre les valeurs des masses volumiques fournies par DensiCal et celles du NIST. Les valeurs sont fournies dans le tableau 1.

6.3.2. Température de vaporisation

  L'objectif du logiciel DensiCal est de calculer des masses volumiques au meilleur niveau d'incertitudes. La courbe de vaporisation est simplement calculée pour déterminer la phase. Pour cette raison un modèle approché a été utilisé pour calculer cette courbe. La validation doit ici permettre de déterminer le seuil d'alerte approprié. La température de vaporisation calculée au moyen de DensiCal a été comparée à 19 valeurs calculées par le NIST [13]. Ces valeurs correspondent à une plage de pressions allant de 611,657 Pa à 22,064 MPa couvrant la totalité de la courbe de vaporisation. Les résultats sont fournis dans le tableau 2. En conservant les résolutions du NIST, l'écart maximum est de 0,008 °C. En conséquence un seuil d'alerte de fusion de 0,01 °C semble approprié.

6.4. Télécharger DensiCal

Références