
 |
Un certain nombre de documents et de logiciels commencent à voir le jour sur la méthode de Monte-Carlo appliquée au calcul des incertitudes. Cette situation fait suite à un guide supplémentaire du GUM [1]. Néanmoins, l'un des points les plus fondamentaux porte sur le choix du générateur de nombres aléatoires. Celui-ci semble très souvent passé sous silence. Pourtant son importance est telle qu'il peut être responsable de résultats erronés.
1. Contexte
La méthode de propagation des distributions selon la méthode de Monte-Carlo nécessite de simuler des échantillons de valeurs pour chacune des grandeurs d'entrée du modèle de la mesure. Traditionnellement, on a un modèle de la mesure faisant intervenir n variables aléatoires X1, ..., Xn auxquelles on a attribué :
À partir de ces données on génère une distribution de laquelle on déduit la valeur moyenne et l'incertitude type u (y) du résultat comme indiqué sur la figure 1.
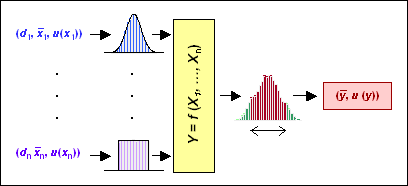
Cette méthode permet évidemment d'avoir un niveau de confiance à partir de la distribution de la variable de sortie et de contourner les problèmes de non linéarité du modèle constatés avec la méthode traditionnelle de propagation des variances. Pour approfondir ce dernier problème le lecteur pourra consulter :
On démontre que pour une variable aléatoire de loi quelconque on peut générer un échantillon de valeurs à partir :
En d'autres termes, la constitution d'échantillons de valeurs pour propager des distributions selon la méthode de Monte-Carlo nécessite à la base de définir un générateur de nombres aléatoires uniforme à valeurs réelles entre 0 et 1.
À ce stade, deux remarques s'imposent concernant le caractère aléatoire des nombres générés et la corrélation entre les valeurs générées. Utiliser un ordinateur pour générer des nombres aléatoires peut paraître en effet déconcertant. N'importe quel programme informatique ne fait qu'exécuter une suite d'instructions écrites à l'avance : en ce sens, le générateur sera forcément déterministe et non véritablement aléatoire. Certains auteurs parlent de « pseudo-hasard » pour qualifier cette situation. D'autre part, toute valeur stockée dans un ordinateur possède un nombre fini de chiffres. En d'autres termes, toute suite de valeurs stockée dans un ordinateur est nécessairement périodique pour un grand nombre de valeurs. Les premiers générateur présentaient d'ailleurs des périodes très courte en raison de l'utilisation de codages limitant la quantité de chiffres contenus dans un nombre : on peut par exemple trouver dans la référence [3] un générateur produisant des nombres aléatoires compris entre 0,000 0 et 0,999 9...
Toute la difficulté est donc de trouver un générateur offrant des valeurs suffisamment aléatoires et de période la plus grande possible compte tenu des
limitations matérielles.
Le premier point peut être résolu en utilisant des tests statistiques pour valider les générateurs
[5].
Le second point dépend en partie du paramétrage du générateur.
La plupart des langages de programmation, des tableurs et des logiciels de simulation numérique possèdent au moins un générateur uniforme de nombres aléatoires.
Le tableau 1 donne une liste non exhaustive de quelques générateurs.
| Nom de la fonction | Commentaire |
| random () | langage Pascal |
| rand () | calculatrices Texas Instruments et HP |
| rd () | / |
| randu () | IBM 360 |
| alea () | Excel |
| rnd () | langage Basic |
| ranf () | Cray |
| drand48 () | Unix |
| Ran# | calculatrices Casio |
De façon générale, il convient d'être extrêmement prudent avec les générateurs intégrés dans les logiciels en l'absence d'informations sur les algorithmes et les codages utilisés. Certains peuvent en effet présenter des périodes courtes, ce qui génère des corrélations entre les variables. Par exemple on peut trouver des générateurs codés sur 32 bits offrant des périodes de l'ordre de 215 (32 768), ce qui devient rapidement insuffisant. En effet, un modèle possédant 10 grandeurs d'influence pour lesquelles on souhaite générer des échantillons de 5 000 valeurs nécessitera de générer au total 50 000 valeurs, soit 17 232 valeurs présentant des corrélations...
Note : il faudrait enfin tordre le cou à une idée reçue qui est de surcroît disséminée par les organismes accréditeurs, les auditeurs et la norme NF/EN 17025 selon laquelle un logiciel dont l'usage est répandu est validé. Cela conduit aujourd'hui à ce que l'on ne remette pas en cause les calculs effectués par le tableur Excel : ce qui est une erreur. Le fait que ce logiciel soit utilisé à grande échelle ne veut pas dire que ses calculs sont exacts, mais simplement que la stratégie commerciale de Microsoft a été efficace. D'ailleurs la plupart des utilisateurs utilisent ce tableur car il était présent sur leur ordinateur avec la suite bureautique Office : combien l'ont acheté pour la fiabilité de ses algorithmes ou l'exactitude de ses résultats ? Et combien l'utilisent parce qu'ils ne veulent pas apprendre à utiliser un autre logiciel, pour son ergonomie ou parce qu'il produit des jolis graphiques ? On pourra se reporter à la référence [4] où on apprend que ce logiciel a quelques difficultés avec les calculs statistiques et que son générateur de nombres aléatoires est dépassé. Enfin les auteurs de cette référence ont constaté que contrairement à beaucoup d'autres logiciels, Microsoft n'a malheureusement pas apporté d'améliorations aux algorithmes statistiques d'Excel suite aux différentes études de fiabilité (pourtant publiées dans des revues scientifiques à comité de lecture).
2. Les générateurs linéaires basés sur la congruence
Ce type de générateur est de loin le plus fréquent dans les langages de programmation. Il peut produire des résultats adaptés pour les besoins d'un calcul d'incertitude courant si sa mise en oeuvre est optimisée (il est possible d'obtenir des périodes de l'ordre de 231 moyennant des algorithmes avec des entiers codés sur 64 bits).
Soit m un entier (le plus grand possible de préférence), a et c deux entiers (avec a non nul). On choisit un entier I0. On calcule ensuite I1 le reste de la division entière de (a·I0 + c) par m. D'après les propriétés de la division, I1 est compris entre 0 et m − 1. D'autre part, toute valeur comprise entre 0 et m − 1 est équiprobable. En répétant cette opération, on génère une suite d'entiers I0, I1, I2, ... tous compris entre 0 et m − 1, distribués de façon équiprobable. En divisant ces valeurs par m, on obtient un échantillon de valeurs réelles distribuées uniformément entre 0 et 1.
Autrement dit, le générateur linéaire basé sur la congruence est défini par la relation suivante :
| \( \left\{ \begin{array}{l} I_{0} \in \mathbb{N} \\ I_{\text{n}+1} = \left( a \cdot I_{\text{n}} + c \right) \mod m \end{array} \right. \) , | (1) |
dans laquelle I0, a, c et m sont des entiers choisis a priori et mod désigne l'opération modulo donnant le reste entier de la division de (a·In + c) par m.
Les contraintes suivantes sont imposées sur les paramètres :
| \( \left\{ \begin{array}{l} m > 0 \\ 0 \leqslant a < m \\ 0 \leqslant c < m \\ 0 \leqslant I_{0} < m \end{array} \right. \) . | (2) |
Le tableau 2 présente les noms donnés usuellement aux différentes variables intervenant dans ce générateur.
| Paramètre | Nom |
| I0 | germe |
| a | multiplicateur |
| c | décalage |
| m | base |
Ensuite, on obtient un échantillon uniforme entre 0 et 1 en calculant :
| \( \begin{eqnarray} u_{\text{n}} = \dfrac{ I_{\text{n} } }{m} \end{eqnarray} \) . | (3) |
Remarque : si on choisit de coder les nombres sur 64 bits, sans astuce de programmation on ne pourra en réalité qu'utiliser des nombres de 32 bits puisque l'opération « a·In » générera un nombre de 64 bits.
Un certain nombre d'études ont été menées pour guider le choix des paramètres afin d'optimiser en particulier la période du générateur ([5] et [6]).
2.2.1. Le générateur de Lehmer (1951)
Les premières études de générateurs ont véritablement commencé au milieu du vingtième siècle avec l'essor de l'informatique. L'un des premiers générateurs a été présenté par Lehmer [7] en 1951. Celui-ci utilisait le paramétrage figurant dans le tableau 3.
| Variable | Valeur |
| a | 23 |
| c | 0 |
| m | 108 + 1 |
Remarque : ce type de générateur faisant intervenir un décalage nul est appelé « générateur multiplicatif ».
Ce générateur est fournit dans le lien suivant : générateurs linéaires.
Un exemple d'échantillon généré par ce programme est reproduit sur la figure 2.
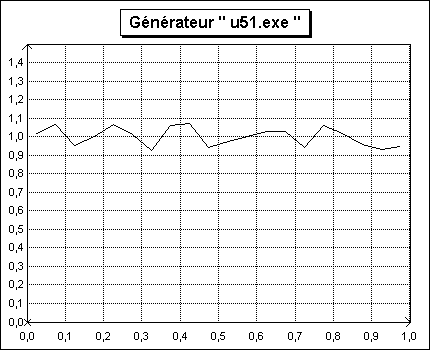
Ce générateur est surtout fournit dans ce dossier pour des raisons historiques. On lui préférera les générateurs de Lewis Goodman et Miller ou de Hill-Wichmann détaillés dans les paragraphes qui suivent.
Note : Le générateur u51.exe a été programmé avec un germe I0 = 10.
2.2.2. Le générateur de Lewis Goodman et Miller (1969)
Le générateur qui suit a été proposé pour la première fois en 1969 par Lewis, Goodman et Miller. Celui-ci présente l'avantage d'être de conception relativement simple et a été utilisé depuis de nombreuses années sans avoir été remis en cause. Le paramétrage de ce générateur est fournit dans le tableau 4.
| Variable | Valeur |
| a | 16 807 |
| c | 0 |
| m | 231 − 1 |
Ce générateur est fournit dans le lien suivant : générateurs linéaires.
Un exemple d'échantillon généré par ce programme est reproduit sur la figure 3.
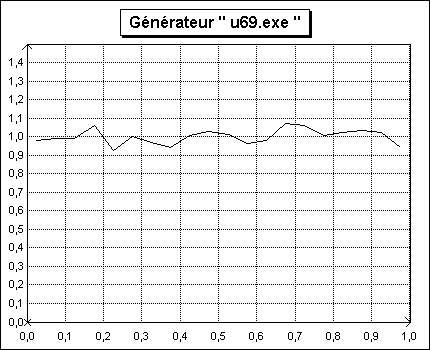
La période de ce générateur est 231 − 2.
Note : Le générateur u69.exe a été programmé avec un germe I0 = 10.
2.2.3. Le générateur de Hill-Wichmann (1982)
Ce générateur recommandé par Hill et Wichmann [8] est en fait la somme de trois générateurs linéaires multiplicatifs basés sur la congruence. Cette méthode permet de créer un générateur de période relativement élevée (6×1012 soit approximativement 242) avec un simple compilateur 16 bits.
Le paramétrage des trois générateurs est fournit dans les tableaux 5, 6 et 7.
| Variable | Valeur |
| a | 171 |
| c | 0 |
| m | 30 269 |
| Variable | Valeur |
| a | 170 |
| c | 0 |
| m | 30 307 |
| Variable | Valeur |
| a | 172 |
| c | 0 |
| m | 30 323 |
On pose Ik, j la ke valeur générée par le je générateur (j ∈ {1 ; 2 ; 3}).
On prend comme conditions initiales :
| \( \left\{ \begin{array}{l} 1 \leqslant I_{0,~1} \leqslant 30~000 \\ 1 \leqslant I_{0,~2} \leqslant 30~000 \\ 1 \leqslant I_{0,~3} \leqslant 30~000 \end{array} \right. \) . | (4) |
Ensuite, on obtient un échantillon uniforme entre 0 et 1 en calculant :
| \( \begin{eqnarray} u_{\text{k}} = \left( \dfrac{I_{\text{k},~1}}{30~269} + \dfrac{I_{\text{k},~2}}{30~307} + \dfrac{I_{\text{k},~3}}{30~323} \right) \mod 1 \end{eqnarray} \) . | (5) |
Remarque : l'opération modulo 1 revient à ne garder que la partie décimale.
Ce générateur est fournit dans le lien suivant : générateurs linéaires.
Un exemple d'échantillon généré par ce programme est reproduit sur la figure 4.
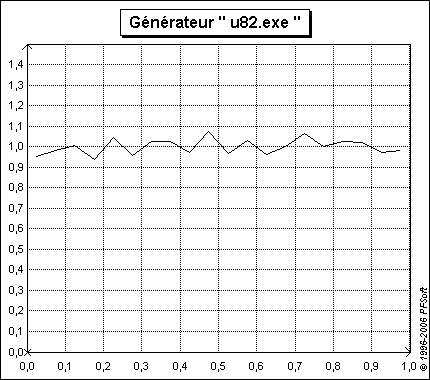
Note : Les trois générateurs de u82.exe ont été programmés avec des germes valant 10, 11 et 12 (respectivement pour le premier le deuxième et le troisième générateur).
3. Cas pratique d'une loi uniforme de moyenne b et de demi étendue a.
Soit U une variable uniforme suivant la loi U (0, 1). On applique la transformation :
| Y = a · (2 · U − 1) + b . | (6) |
On montre que la variable aléatoire Y suit la loi U (b, a).
Le programme uniform.exe figurant dans le lien ci-dessous permet de transformer un échantillon généré par l'un des générateurs uniforme de ce dossier (u51, u69 ou u82) en un échantillon de moyenne b et de demi étendue a.
 |
Ce programme s'utilise en ligne de commande en employant la syntaxe suivante :
| uniform.exe a b "source" "destination" |
avec :
a : la demi étendue voulue ;
b : la moyenne voulue ;
source : le nom du fichier généré par
u51, u69 ou
u82 ;
destination : le nom du fichier à créer.
4. Conclusions et perspectives
La méthode de Monte-Carlo permet de contourner les problèmes de non linéarité et permet d'attribuer un niveau de confiance à une incertitude mais introduit de nouvelles difficultés. L'une des principales est la génération de nombres aléatoires. Tout les calculs reposent à la base sur la génération de nombres suivant une distribution uniforme. L'histoire encore récente sur les méthodes de génération de nombres aléatoires montre que tous les générateurs ne se valent pas et que la façon de les programmer influe significativement sur leurs performances. En d'autres termes, on ne devra pas tenir pour acquis les résultats d'un logiciel ou d'une publication qui ne mentionnent pas clairement quel est le générateur employé et quel germe a été employé afin de garantir une certaine " traçabilité des calculs " (par exemple dans certaines publications on peut simplement lire qu'un générateur linéaire basé sur la congruence a été utilisé ; c'est évidemment insuffisant). D'autre part, les sources des programmes étant rarement accessible, il faudra envisager de mettre en oeuvre des dossier de validation des générateurs sur les logiciels employés.
| [1] | JCGM, "Evaluation of measurement data - Supplement 1 to the "Guide to the expression of uncertainty in measurement" - Propagation of distributions using a Monte-Carlo method", BIPM, JCGM 101:2008, 2008, www.bipm.org. |
| [2] | GONZALEZ A.G., HERRADOR A.A., ASUERO A.G., "Uncertainty evaluation from Monte-Carlo simulations by using Crystal-Ball software", Accred Qual Assur, 10, Springer, 2005. |
| [3] | LOHNES P.R., COOLEY W.W, "Introduction to statistical Procedures: with Computer Exercises", John Wiley & Sons Inc, New York, 1968. |
| [4] | MCCULLOUGH D.B., WILSON B., "On the accuracy of statistical procedures in Microsoft Excel 2000 and XP", Computational Statistics & Data Analysis, vol. 40, 3, 325-332, 2002. |
| [5] | KNUTH D.E., "Seminumerical Algorithms - 3rd ed. - The Art of Computer Programming", vol. 2, Addison-Wesley, Reading, Massachusetts, 1998. |
| [6] | RIPLEY B.D., "Stochastic Simulation", Wiley, New York, 1987. |
| [7] | LEHMER D.H., "Mathematical methods in large-scale computing units", Proceedings of the Second Symposium on Large-Scale Digital Calculating Machinery, Harvard University Press, Cambridge, Massachusetts, 141-146, 1951. |
| [8] | HILL I.D. et WICHMANN B., "Algorithm AS 183: An efficient and portable pseudo-random number generator", Applied Statistics, 31, 188-190, 1982. |