
 |
Ce dossier fait suite à plusieurs remarques concernant le logiciel Gumy [1]. Un certain nombre d'utilisateurs ont en effet regretté l'absence de calcul automatique des dérivées sur le logiciel Gumy pour évaluer les coefficients de sensibilité lors de l'application de la loi de propagation des incertitudes. L'ajout de cette fonction n'a pas été jugée souhaitable par l'auteur du logiciel car elle pourrait masquer à l'utilisateur le détail des calculs, ce qui ne correspond pas à la philosophie de Gumy qui est avant tout un assistant pour suivre une démarche rationnelle lors des calculs d'incertitudes. Ceci étant il est vrai que lorsqu'on a perdu l'habitude de calculer des dérivées, la détermination des coefficients de sensibilité peut rapidement devenir fastidieuse. Plutôt que de donner une table des dérivées, comme cela est fait dans de nombreuses formations, il a été estimé plus constructif et pragmatique de réaliser un logiciel se présentant sous la forme d'une calculatrice permettant de calculer les dérivées sous forme symbolique et de les évaluer. Ces dérivées sous forme symbolique pourront également être enregistrées sur disque et être accessible par lien hypertexte depuis Gumy. Et plus généralement, ce logiciel pourra servir à toute personne devant par exemple calculer des dérivées.
2. Le logiciel PFS-Algebraic Calculator (PFS-AC)
Comme dit précédemment le logiciel PFS-AC se présente sous la forme d'une calculatrice (cf. fig. 1). Celui-ci permet de saisir sous forme symbolique des équations, de les évaluer et également de procéder à la dérivation symbolique de ces équations.
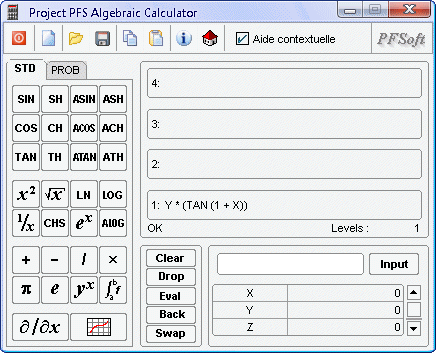
L'interface de travail de PFS-AC est divisée en cinq zones de travail repérées de A à E et détaillées ci-dessous :
A La barre d'outils

 |
Fermer le logiciel (pensez à sauvegarder votre fonction) |
 |
Créer une nouvelle fonction (cette option efface la pile et réinitialise les variables contrairement à Clear) |
 |
Charger une fonction enregistrée sur disque (les fichiers PFS-AC portent l'extension .fct) |
 |
Enregistrer la fonction sur le disque (l'ensemble des variables est également sauvegardé) |
 |
Copier le texte sélectionné |
 |
Coller le presse papier |
 |
Afficher les informations sur le logiciel PFS-AC |
 |
Lancer le navigateur et afficher le site internet MetGen.org |
L'option aide contextuelle permet d'afficher des bulles d'aide lorsque la souris parcours les boutons. Pour un utilisateur habitué au logiciel, cette fonction peut devenir agaçante et peut donc être désactivée.
B La zone de saisie des opérations et constantes
Onglet 'Standard' (STD)
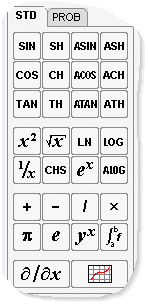 |
Cette zone contient les principales fonctions disponibles sur PFS-AC énumérées ci-dessous (les fonctions monadiques nécessitent un
niveau de pile, les fonctions et opérations dyadiques nécessitent deux niveaux).
|
||
|
|||
|
La zone B contient également l'opérateur \( \partial / \partial x \) qui permet de dériver symboliquement le dernier niveau de la pile. |
|||
Onglet 'Probabilités' (PROB)
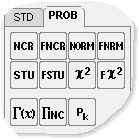 |
Cette zone contient quelques fonctions utiles pour le calcul des
probabilités. Les fonctions triadiques nécessitents trois niveaux de pile.
Fonctions monadiques : NCR : fonction de répartition de la loi normale centrée réduite [NCR (x)] FNCR : fractile unilatéral de la loi normale centrée réduite [FNCR (p)] Γ(x) : fonction gamma d'Euler [GAMMA (x)] Note 1 : la fonction gamma n'est pas à proprement parler une fonction rattachée aux probabilités. Néanmoins, elle a été incluse ici car elle sert aussi au calculs sur la loi de Student. Note 2 : quelques fois on dit que cette fonction est la fonction factorielle pour les nombres réels. Ceci n'est pas tout à fait exact, mais on peut démontrer que la fonction Γ (x + 1) est un prolongement par continuité la fonction factorielle (x!) sur \( \mathbb{R} \). PK : probabilité Pk du critère de Chauvenet [PK (tk)] (cf. [2]) Fonctions dyadiques : STU : fonction de répartition de la loi de Student [STU (ν ; x)] FSTU : fractile unilatéral de la loi de Student [FSTU (ν ; p)] χ2 : fonction de répartition de la loi du χ2 [KHI2 (ν ; x)] Fχ2 : fractile unilatéral de la loi du χ2 [FKHI2 (ν ; p)] ΓINC : fonction gamma incomplète [GAMMAINC (x ; a)] Fonctions triadiques : NORM : fonction de répartition de la loi normale [NORM (m ; s ; x)] FNORM : fractile unilatéral de la loi normale [FNORM (m ; s ; p)] |
C La pile
 |
La pile mémoire de PFS-AC est infinie, néanmoins cette version du logiciel ne permet d'afficher que les quatre derniers niveaux. |
D La zone de manipulation de la pile
 |
Cette zone contient les instructions de manipulation de la pile énumérées ci-dessous (les instructions sont en anglais pour les utilisateurs habitués
aux calculatrices HP).
Clear : efface l'ensemble de la pile (rq : les variables ne sont pas affectées) Drop : efface le dernier niveau de la pile (niveau « 1: ») Eval : évalue l'expression du dernier niveau de la pile Back : efface le dernier pas saisi Swap : permute les deux derniers niveaux de la pile |
E La zone de saisie clavier et des variables
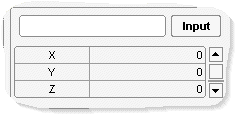 |
Cette zone permet d'une part de saisir des valeurs au clavier puis de les insérer dans la pile en cliquant sur Input,
et d'autre part de visualiser, de saisir et d'insérer des variables dans la pile ou leur valeurs.
Pour modifier le nom d'une variable, cliquez sur son symbole avec le bouton droit de la souris et saisissez son nouveau nom. Procédez de même pour sa valeur. Pour insérer une variable dans la pile cliquez sur son symbole avec le bouton gauche de la souris. |
4. Exemple d'utilisation de PFS-AC
Calculons par exemple la dérivée de cos [tan (x + 1)] puis évaluons la en
π / 3.
Tout d'abord précisons que PFS-AC utilise la notation polonaise inversée (RPN : Reverse Polish Notation). Par exemple, dans ce système de notation,
utilisé en particulier sur les calculatrices HP, l'addition 'a + b' s'écrit
'a b +'.
| Action | Pile |
| Etape 1 : saisie de cos (tan (x + 1)) | |
| Cliquez sur X dans la zone E | 4: |
| 3: | |
| 2: | |
| 1: X | |
| Saisissez '1' dans la zone E puis cliquez sur Input | 4: |
| 3: | |
| 2: X | |
| 1: 1 | |
| Cliquez sur \( + \) dans la zone B | 4: |
| 3: | |
| 2: | |
| 1: X + 1 | |
| Cliquez sur TAN dans la zone B | 4: |
| 3: | |
| 2: | |
| 1: TAN (X + 1) | |
| Cliquez sur COS dans la zone B | 4: |
| 3: | |
| 2: | |
| 1: COS (TAN (X + 1)) | |
| Etape 2 : calcul de la dérivée de cos (tan (x + 1)) | |
| Cliquez sur \( \partial / \partial x \) dans la zone B et sélectionnez la variable 'X' dans l'assistant de dérivation | 4: |
| 3: | |
| 2: | |
| 1: (CHS (SIN (TAN (X + 1)))) * (1 + (SQ (TAN (X + 1)))) | |
| Etape 3 : évaluation de la dérivée en π/ 3 | |
| Cliquez avec le bouton droit de la souris sur la valeur en face de X dans la zone E puis saisissez la valeur numérique de π / 3. | 4: |
| 3: | |
| 2: | |
| 1: (CHS (SIN (TAN (X + 1)))) * (1 + (SQ (TAN (X + 1)))) | |
| Cliquez sur le bouton Eval dans la zone D | 4: |
| 3: | |
| 2: (CHS (SIN (TAN (X + 1)))) * (1 + (SQ (TAN (X + 1)))) | |
| 1: 4,43844114688012 | |
Conclusion :
Le logiciel PFS-AC renvoie la formule de la dérivée : (CHS (SIN (TAN (X + 1)))) * (1 + (SQ (TAN (X + 1)))),
i.e. :
\( \begin{eqnarray} \dfrac{\partial}{\partial x}\left( \cos \left( \tan \left( x + 1 \right) \right) \right) = -\sin \left[\tan (x + 1)\right] \cdot \left[1 + (\tan (x + 1)^{2}\right] \end{eqnarray} \) ,
et sa valeur en π / 3 vaut 4,438 441 146 880 12...
Note : Il peut arriver que lors des calculs de dérivées, les résultats ne soient pas complètement simplifiés. Cela tient au fait que la simplification des expressions numériques est l'un des problèmes les plus délicats du calcul formel. Nos habitudes de calcul et notre savoir-faire ne sont effectivement pas toujours faciles à transposer sur machine.
| [1] | PLATEL F., « Calcul d'incertitudes avec Gumy », MetGen, Dossier métrologie 4. |
| [2] | PLATEL F., « Elimination de mesures - Le critère de Chauvenet », MetGen, Dossier métrologie 15. |