
 |
Toute personne ayant effectué des mesures de répétabilité
a forcément été confrontée un jour à une mesure
« suspecte ». « Suspecte » parce qu'elle semblait
s'éloigner beaucoup trop des autres mesures, ce qui incitait à penser
qu'une erreur était survenue lors de la mesure. Il est toutefois délicat
d'éliminer une valeur puisque les probabilités nous enseignent que dans le
cas d'une loi normale toute valeur est possible. Ainsi le fait de retirer une valeur au
motif qu'elle semble trop s'éloigner des autres pourrait alors être
perçu comme une forme de malhonnêteté scientifique, une volonté
de « trafiquer » des résultats (en particulier pour améliorer
l'incertitude). Dans une pareille situation, il faudrait idéalement analyser la
mesure effectuée pour déceler une éventuelle erreur ou effectuer un
grand nombre de mesures supplémentaires pour la confirmer ou l'infirmer (ce qui
justifierait alors son retrait). Cela n'est malheureusement pas toujours possible.
Le critère de Chauvenet apporte une réponse robuste à ce
problème en considérant la probabilité d'obtenir la mesure
jugée suspecte. Toutefois, il importe de conserver à l'esprit que la
décision finale de conserver ou supprimer une mesure est de la responsabilité
de l'opérateur.
Soit {x1, …,
xn} un ensemble de n
mesures et k  {1, …, n}.
Supposons que l'on ait un doute sur la mesure xk.
{1, …, n}.
Supposons que l'on ait un doute sur la mesure xk.
On commence par calculer la moyenne ( ) et l'écart
type
) et l'écart
type  x)
de l'échantillon :
x)
de l'échantillon :
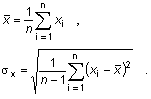 |
Ensuite, on calcule le nombre d'écarts types (tk) par lesquels la valeur suspecte s'éloigne de la moyenne :
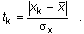 |
Puis on calcule la probabilité (Pk) d'obtenir la valeur xk à l'aide du tableau 1.
| tk | 0,00 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 |
| 0,0 | 0,00 | 0,80 | 1,60 | 2,40 | 3,20 | 3,98 | 4,78 | 5,58 | 6,38 | 7,18 |
| 0,1 | 7,96 | 8,76 | 9,56 | 10,34 | 11,14 | 11,92 | 12,72 | 13,50 | 14,28 | 15,06 |
| 0,2 | 15,86 | 16,64 | 17,42 | 18,20 | 18,96 | 19,74 | 20,52 | 21,28 | 22,06 | 22,82 |
| 0,3 | 23,58 | 24,34 | 25,10 | 25,86 | 26,62 | 27,36 | 28,12 | 28,86 | 29,60 | 30,34 |
| 0,4 | 31,08 | 31,82 | 32,56 | 33,28 | 34,00 | 34,72 | 35,44 | 36,16 | 36,88 | 37,58 |
| 0,5 | 38,30 | 39,00 | 39,70 | 40,38 | 41,08 | 41,76 | 42,46 | 43,14 | 43,80 | 44,48 |
| 0,6 | 45,14 | 45,80 | 46,48 | 47,14 | 47,78 | 48,44 | 49,08 | 49,72 | 50,34 | 50,98 |
| 0,7 | 51,60 | 52,22 | 52,84 | 53,46 | 54,08 | 54,68 | 55,28 | 55,88 | 56,46 | 57,04 |
| 0,8 | 57,62 | 58,20 | 58,78 | 59,34 | 59,90 | 60,46 | 61,02 | 61,56 | 62,12 | 62,66 |
| 0,9 | 63,18 | 63,72 | 64,24 | 64,76 | 65,28 | 65,78 | 66,30 | 66,80 | 67,30 | 67,78 |
| 1,0 | 68,26 | 68,76 | 69,22 | 69,70 | 70,16 | 70,62 | 71,08 | 71,54 | 71,98 | 72,42 |
| 1,1 | 72,86 | 73,30 | 73,72 | 74,16 | 74,58 | 74,98 | 75,40 | 75,80 | 76,20 | 76,60 |
| 1,2 | 76,98 | 77,38 | 77,76 | 78,14 | 78,50 | 78,88 | 79,24 | 79,60 | 79,94 | 80,30 |
| 1,3 | 80,64 | 80,98 | 81,32 | 81,64 | 81,98 | 82,30 | 82,62 | 82,94 | 83,24 | 83,54 |
| 1,4 | 83,84 | 84,14 | 84,44 | 84,72 | 85,02 | 85,30 | 85,58 | 85,84 | 86,12 | 86,38 |
| 1,5 | 86,64 | 86,90 | 87,14 | 87,40 | 87,64 | 87,88 | 88,12 | 88,36 | 88,58 | 88,82 |
| 1,6 | 89,04 | 89,26 | 89,48 | 89,68 | 89,90 | 90,10 | 90,30 | 90,50 | 90,70 | 90,90 |
| 1,7 | 91,08 | 91,28 | 91,46 | 91,64 | 91,82 | 91,98 | 92,16 | 92,32 | 92,50 | 92,66 |
| 1,8 | 92,82 | 92,98 | 93,12 | 93,28 | 93,42 | 93,56 | 93,72 | 93,86 | 93,98 | 94,12 |
| 1,9 | 94,26 | 94,38 | 94,52 | 94,64 | 94,76 | 94,88 | 95,00 | 95,12 | 95,22 | 95,34 |
| 2,0 | 95,44 | 95,58 | 95,66 | 95,76 | 95,86 | 95,96 | 96,06 | 96,16 | 96,24 | 96,34 |
| 2,1 | 96,42 | 96,52 | 96,60 | 96,68 | 96,76 | 96,84 | 96,92 | 97,00 | 97,08 | 97,14 |
| 2,2 | 97,22 | 97,28 | 97,36 | 97,42 | 97,50 | 97,56 | 97,62 | 97,68 | 97,74 | 97,80 |
| 2,3 | 97,86 | 97,92 | 97,96 | 98,02 | 98,08 | 98,12 | 98,18 | 98,22 | 98,26 | 98,32 |
| 2,4 | 98,36 | 98,40 | 98,44 | 98,50 | 98,54 | 98,58 | 98,62 | 98,64 | 98,68 | 98,72 |
| 2,5 | 98,76 | 98,80 | 98,82 | 98,86 | 98,90 | 98,92 | 98,96 | 98,98 | 99,02 | 99,04 |
| 2,6 | 99,06 | 99,10 | 99,12 | 99,14 | 99,18 | 99,20 | 99,22 | 99,24 | 99,26 | 99,28 |
| 2,7 | 99,30 | 99,32 | 99,34 | 99,36 | 99,38 | 99,40 | 99,42 | 99,44 | 99,46 | 99,48 |
| 2,8 | 99,48 | 99,50 | 99,52 | 99,54 | 99,54 | 99,56 | 99,58 | 99,58 | 99,60 | 99,62 |
| 2,9 | 99,62 | 99,64 | 99,64 | 99,66 | 99,68 | 99,68 | 99,70 | 99,70 | 99,72 | 99,72 |
On calcule enfin le nombre théorique de valeurs (nk) correspondant que l'on devrait avoir dans l'échantillon par la formule :
| nk = n × Pk . |
D'après le critère de Chauvenet, xk peut être éliminée si nk < 0,5.
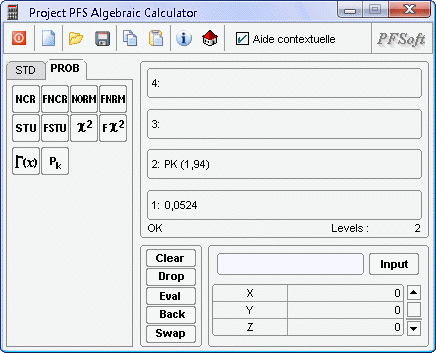
On peut également obtenir Pk directement à l'aide du logiciel PFS-AC [2] en utilisant la fonction 'PK ()' disponible dans l'onglet 'PROB' comme indiqué sur la figure 1 (ce qui dispense d'effectuer des interpolations avec le tableau 1).
Supposons que la mesure de la température d'un bain à l'aide d'un thermomètre à dilatation donne les valeurs reproduites dans le tableau 2.
| Mesure n° i | Valeur xi |
| 1 | 35,9 °C |
| 2 | 36,0 °C |
| 3 | 36,0 °C |
| 4 | 36,2 °C |
| 5 | 36,1 °C |
| 6 | 35,2 °C |
La valeur x6 = 35,2 °C
est jugée « suspecte ». Peut-on l'éliminer ?
On commence par caluler la moyenne et l'écart type :
 = 35,9 °C , = 35,9 °C ,
 x = 0,36 °C . x = 0,36 °C .
|
Puis on calcule :
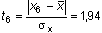 |
ce qui permet de déduire, d'après le tableau 1 :
P6 = 1 - 94,76 / 100 = 0,052 4 .
Donc n6 = 0,3 < 0,5.
Par conséquent, la mesure peut être éliminée.
Note : il convient toutefois d'être prudent car dans le cas présent, une telle anomalie pourrait très bien être due à une colonne de mercure fractionnée dans le thermomètre, auquel cas l'ensemble des mesures seraient fausses…
| [1] | "Tables statistiques", Revue de Statistique Appliquée, 1973. |
| [2] | PLATEL F., « Calcul symbolique sur ordinateur - Projet PFS-Algebraic Calculator », MetGen, Dossier divers 2. |