
 |
En métrologie, un certain nombre de logiciels d'acquisition
proposent de corriger automatiquement les indications brutes des instruments de mesure.
C'est par exemple le cas des logiciels associés aux centrales d'acquisition
utilisées pour la caractérisation des enceintes thermostatiques ou de
certains thermomètres calibrateurs portatifs. Néanmoins, ces appareils ou
logiciels ne saisissent pas directement la table d'étalonnage mais demandent un
polynôme de correction.
L'objet de ce dossier est de présenter une approche
algébriste des polynômes des moindres carrés. Très souvent les
physiciens les déterminent en minimisant une fonction d'écart par des
méthodes relevant de l'analyse. Cela peut certes suffire, mais on peut
également les obtenir par des méthodes algébristes en projetant le
vecteur des observations sur un espace vectoriel engendré par des polynômes
bien choisis avec un produit scalaire approprié. L'approche algébriste
permet en particulier d'introduire très simplement la notion de
pondération sur les variables. En effet, les données issues d'un
étalonnage sont entachées d'incertitudes qui traduisent une plus ou
moins grande confiance dans ces données : il est alors logique qu'elles
n'aient pas toutes la même influence dans les calculs.
L'approche présentée ici dans un cadre déterministe
- pourtant indispensable à toute fonction métrologique industrielle de base -
semble complètement occultée par la littérature métrologique.
Enfin, la méthode étant un peu lourde à mettre en oeuvre,
la troisième partie de ce dossier propose un logiciel gratuit (PolyReg)
permettant le calcul de polynômes des moindres carrés pondérés.
Ce logiciel permet une représentation graphique de
résultats d'étalonnage avec la visualisation des incertitudes. Enfin, il
permet également de corriger des résultats d'étalonnage bruts de
manière automatique, cette option présente un intérêt pour des
caractérisation d'enceintes thermostatiques ou il faut souvent corriger les
données « au kilomètre ».
2.1. Détermination du polynôme
Soient \(n\) un entier strictement supérieur à 1 et
\( F = \{(x_\text{i}, y_\text{i}) \in \mathbb{R}^{2}, i \in [1 \ldots n]\} \),
un ensemble de \(n\) observations et \(p\) un entier strictement inférieur à \(n\).
On cherche le polynôme \(P\) à coefficients réels
noté :
| \( \begin{eqnarray}P(x) = a_0 + a_1 \cdot x + a_2 \cdot x^{2} + \ldots + a_\text{p} \cdot x^\text{p}\end{eqnarray} \) , |
|
pour lequel la quantité :
| \( \begin{eqnarray}\sum_{\text{i} = 1}^\text{n} (P(x_\text{i}) - y_\text{i})^{2}\end{eqnarray} \) | |
est minimale.
En posant :
| \( \begin{eqnarray}X = \begin{pmatrix} {1} & {x_1} & {x_1^2} & {\ldots} & {x_1^\text{p}} \\ {1} & {x_2} & {x_2^2} & {\ldots} & {x_2^\text{p}} \\ {.} & & & & {.} \\ {.} & & & & {.} \\ {.} & & & & {.} \\ {1} & {x_\text{n}} & {x_\text{n}^2} & {\ldots} & {x_\text{n}^\text{p}} \\ \end{pmatrix} \quad \mbox{,} \quad Y = \begin{pmatrix} {y_1} \\ {y_2} \\ {.} \\ {.} \\ {.} \\ {y_\text{n}} \\ \end{pmatrix} \quad \mbox{et} \quad \widehat{\beta} = \begin{pmatrix} {a_0} \\ {a_1} \\ {.} \\ {.} \\ {.} \\ {a_\text{p}} \\ \end{pmatrix}\end{eqnarray} \) | |
le problème posé revient alors à trouver un vecteur \( \beta \) minimisant la norme de \( (X \times \beta - Y) \). On note \( \widehat{\beta} \) le vecteur minimisant cette norme (cf. figure 1).
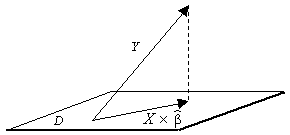
Soit \( D = \{ X \times \beta, \quad \beta \in \mathbb{R}^\text{p} \} \). De façon triviale, \( D \) est un sous espace vectoriel de \( \mathbb{R}^\text{p} \). D'après le théorème de Pythagore, \( \widehat{\beta} \) est tel que le vecteur \( (Y - X \times \widehat{\beta}) \) appartient à l'orthogonal de \( D \).
Soit \( \beta \) un élément de \( \mathbb{R}^\text{p} \). On note \( (.|.) \) le produit scalaire euclidien. D'après ce qui précède :
| \( \begin{eqnarray}(X \times \beta \;\; | \;\; (Y - X \times \widehat{\beta} )) = 0\end{eqnarray} \) , | |
en notant \( ^\text{t}(.) \) l'opération de transposition, on a successivement :
| \( \begin{eqnarray}^\text{t}(X \times \beta) \times (Y - X \times \widehat{\beta}) = 0\end{eqnarray} \) \( \begin{eqnarray}^\text{t}\beta \times (^\text{t}X \times Y - ^\text{t}X \times X \times \widehat{\beta}) = 0\end{eqnarray} \) |
|
Ceci étant vrai pour tout vecteur \( \beta \), on obtient :
| \( \begin{eqnarray}^\text{t}X \times Y - ^\text{t}X \times X \times \widehat{\beta} = 0\end{eqnarray} \) | |
Si \( (^\text{t}X \times \ X) \) est inversible, alors :
| \( \begin{eqnarray}\widehat{\beta} = (^\text{t}X \times X )^{-1} \times ^\text{t}X \times Y\end{eqnarray} \) . | (1) |
Les données étant souvent entachées d'incertitudes
(a priori différentes) il est alors tentant d'accorder plus d'importance
aux données ayant de faibles incertitudes, dont la connaissance est de ce fait plus
assurée, qu'aux valeurs présentant de mauvaises incertitudes. Cela
pourra conduire par exemple à minimiser l'influence de valeurs issues de
conditions extrêmes, proches des limites des instruments de mesure.
Soit \( \{w_\text{i}, i \in [1 \ldots n]\} \) un ensemble de \( n \) réels positifs ou nuls tels que
pour \( i \in [1 \ldots n] \), \( w_\text{i} \) représente le degré de confiance que l'on a sur l'exactitude
du doublet \( (x_\text{i}, y_\text{i}) \). Pour prendre en compte l'influence de la pondération
dans l'approximation il suffit de multiplier chacune des composante de \( X \) et de
\( Y \) par la racine carrée de la pondération qui lui est associée.
Pratiquement, cela revient
à construire la matrice diagonale \( W_{1/2} \)
avec les racines carrées des valeurs \( w_\text{i} \)
sur la diagonale et des 0 ailleurs, puis à remplacer \( X \) par
\( (W_{1/2} \times X) \) et \( Y \) par \( (W_{1/2} \times Y) \).
La simplicité de cette prise en compte de la
pondération résulte de la linéarité du formalisme matriciel
employé.
Les calculs se simplifient et la formule (1) avec prise en compte de la
pondération devient :
| \( \begin{eqnarray}\widehat{\beta} = (^\text{t}X \times W \times X)^{-1} \times ^\text{t}X \times W \times Y\end{eqnarray} \) , | (2) |
avec :
| \( \begin{eqnarray}W = \begin{pmatrix} w_1 & & & & & \\ & w_2 & & & 0 & \\ & & . & & & \\ & & & . & & \\ & 0 & & & . & \\ & & & & & w_\text{n} \\ \end{pmatrix}\end{eqnarray} \) |
La difficulté est maintenant de choisir une pondération. Afin de tenir compte des incertitudes, on pourra prendre par exemple comme valeurs de pondération pour le doublet d'observations \( (x_\text{i}, y_\text{i}) \) avec \( i \in \{1, \ldots, n\} \) :
| \( \begin{eqnarray}w_i = \frac{ \frac{1}{U_\text{i}^2} }{ \sum_{ \text{j} = 1 }^{\text{n}} \frac{1}{U_\text{j}^2} }\end{eqnarray} \) | (3) |
\( U_\text{k} \) étant l'incertitude élargie sur \( y_\text{k} \; (k \in \{1, \ldots, n\}) \).
Il convient néanmoins de garder à l'esprit que la
pondération est ici présentée dans un cadre purement
déterministe et non probabiliste.
2.3. Choix du degré du polynôme
Soit \( n \geqslant 2 \) le nombre de doublets numériques \( (x, y) \).
Le degré \( k \) du polynôme calculé pourra
être compris entre 0 et \( (n - 1) \). S'il est aisé
d'éliminer les cas triviaux \( k = 0 \) et \( k = 1 \),
il est moins évident de déterminer à partir de quelle valeur de
\( k \) l'approximation est optimale. Il n'existe en effet pas de méthode
permettant de déterminer le degré du polynôme
« optimum » dans le cas général.
On peut néanmoins remarquer que lorsque l'on augmente le
degré \( k \) du polynôme, les résidus
| \( \begin{eqnarray}R_\text{i} = |y_\text{i} - P_\text{k}(x_\text{i})| \quad (i \in \{0, \ldots, n\})\end{eqnarray} \) |
sont de plus en plus petits. Toutefois, lorsque \( k \) augmente, la proximité du
graphe de \( P \) aux points \( (x_\text{i}, y_\text{i}) \)
s'accompagne souvent d'oscillations en dehors des points d'interpolation qui
sont le plus souvent peu crédibles sur le plan de la physique. Cette remarque souligne
l'importance de systématiquement utiliser un outil de représentation
graphique tel que PolyReg, qui est présenté plus loin dans ce dossier.
Dans le cas ou le modèle physique qui lie \( y_\text{i} \)
à \( x_\text{i} \) est un polynôme (cas des relations entre la
résistance d'une sonde de platine et la température par exemple) dont on
connaît le degré on peut tracer
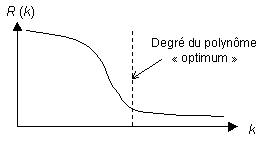
| \( \begin{eqnarray}R(k) = \sum_{ \text{i} = 1 }^{\text{n}} (y_\text{i} - P_\text{k} (x_\text{i}))^2\end{eqnarray} \) |
en fonction de \( k \). Lorsque le degré « optimum » du polynôme sera atteint on observera alors une décroissance rapide de la courbe comme indiqué sur la figure 2.
2.4. Justesse « algébrique » du polynôme
La justesse du polynôme au sens algébrique dépend de la « proximité » entre \( (W_{1/2} \times X \times \widehat{\beta}) \) et \( (W_{1/2} \times Y) \). Cette proximité peut être caractérisée par le cosinus de l'angle formé entre \( W_{1/2} \times X \times \widehat{\beta} \) et \( W_{1/2} \times Y \). Celui-ci se calcule par la formule :
| \( \begin{eqnarray}\cos (\theta) = \frac{ (W_{1/2} \times Y \; | \; W_{1/2} \times X \times \widehat{\beta})}{ \lVert W_{1/2} \times Y \rVert \; \cdot \; \lVert W_{1/2} \times X \times \widehat{\beta}) \rVert }\end{eqnarray} \) |
ce qui s'écrit
| \( \begin{eqnarray}\cos (\theta) = \frac{ ^\text{t}Y \times W \times X \times \widehat{\beta} }{ \sqrt{ ^\text{t}Y \times W \times Y} \; \cdot \; \sqrt{ ^\text{t}\widehat{\beta} \times ^\text{t}X \times W \times X \times \widehat{\beta}} }\end{eqnarray} \) |
Le polynôme sera d'autant plus « juste » que la valeur de \( \lvert \cos \theta \rvert \) sera proche de 1.
2.5. Cas du polynôme du premier degré
En conservant les notations précédentes, ce cas de figure revient à prendre \( p = 1 \). Dès lors les données pour le calcul du polynôme deviennent :
|
Le calcul de \( a_0 \) et \( a_1 \) est effectué dans un premier temps pour des données non pondérées à l'aide de la formule (1). On a alors successivement :
| \( \begin{eqnarray}^\text{t}X \times X = \begin{pmatrix} { \sum_{\text{i} = 1}^{\text{n}} x_\text{i} } & { \sum_{\text{i} = 1}^{\text{n}} x_\text{i}^2 } \\ { n } & { \sum_{\text{i} = 1}^{\text{n}} x_\text{i} } \\ \end{pmatrix}\end{eqnarray} \) , |
puis, si cette matrice est inversible
| \( \begin{eqnarray}(^\text{t}X \times X)^{-1} = \frac{ 1 }{ (\sum_{ \text{i} = 1 }^\text{n} x_\text{i})^2 - n \cdot \sum_{ \text{i} = 1 }^\text{n} x_\text{i}^2 } \times \begin{pmatrix} { \sum_{\text{i} = 1}^{\text{n}} x_\text{i} } & { - \sum_{\text{i} = 1}^{\text{n}} x_\text{i}^2 } \\ { - n } & { \sum_{\text{i} = 1}^{\text{n}} x_\text{i} } \\ \end{pmatrix}\end{eqnarray} \) , |
et d'autre part
| \( \begin{eqnarray}^\text{t}X \times Y = \begin{pmatrix} { \sum_{\text{i} = 1}^{\text{n}} x_\text{i} y\text{i} } \\ { \sum_{\text{i} = 1}^{\text{n}} y_\text{i} } \\ \end{pmatrix}\end{eqnarray} \) , |
ce qui donne finalement :
| \( \begin{eqnarray}(^\text{t}X \times X)^{-1} \times ^\text{t}X \times Y = \frac{ 1 }{ (\sum_{ \text{i} = 1 }^\text{n} x_\text{i})^2 - n \cdot \sum_{ \text{i} = 1 }^\text{n} x_\text{i}^2 } \times \begin{pmatrix} { \sum_{\text{i} = 1}^{\text{n}} x_\text{i} y_\text{i} \; \cdot \; \sum_{\text{i} = 1}^{\text{n}} x_\text{i} \; - \; \sum_{\text{i} = 1}^{\text{n}} x_\text{i}^2 \; \cdot \; \sum_{\text{i} = 1}^{\text{n}} y_\text{i}} \\ { \sum_{\text{i} = 1}^{\text{n}} x_\text{i} \; \cdot \; \sum_{\text{i} = 1}^{\text{n}} y_\text{i} \; - \; n \; \cdot \; \sum_{\text{i} = 1}^{\text{n}} x_\text{i} y_\text{i} } \\ \end{pmatrix}\end{eqnarray} \) , |
autrement dit :
| \( \begin{eqnarray}a_0 = \frac{ \sum_{\text{i} = 1}^{\text{n}} x_\text{i}^2 \; \cdot \; \sum_{\text{i} = 1}^{\text{n}} y_\text{i} \; - \; \sum_{\text{i} = 1}^{\text{n}} x_\text{i} y_\text{i} \;\cdot \; \sum_{\text{i} = 1}^{\text{n}} x_\text{i} }{ n \; \cdot \; \sum_{\text{i} = 1}^{\text{n}} x_\text{i}^2 \; - \; (\sum_{\text{i} = 1}^{\text{n}} x_\text{i})^2 }\end{eqnarray} \) , |
| \( \begin{eqnarray}a_1 = \frac{ n \; \cdot \; \sum_{\text{i} = 1}^{\text{n}} x_\text{i} y_\text{i} \; - \; \sum_{\text{i} = 1}^{\text{n}} x_\text{i} \;\cdot \; \sum_{\text{i} = 1}^{\text{n}} y_\text{i} }{ n \; \cdot \; \sum_{\text{i} = 1}^{\text{n}} x_\text{i}^2 \; - \; (\sum_{\text{i} = 1}^{\text{n}} x_\text{i})^2 }\end{eqnarray} \) . |
On retrouve donc bien les formules habituelles de la droite des moindres carrés que l'on peut trouver par exemple dans la référence [1].
De même le calcul pour des données pondérées donne successivement :
| \( \begin{eqnarray}(^\text{t}X \times W \times X)^{-1} = \frac{ 1 }{ \sum_{ \text{i} = 1 }^{\text{n}} w_\text{i} \; \cdot \; \sum_{ \text{i} = 1 }^{\text{n}} w_\text{i} x_\text{i}^2 \; - \; (\sum_{ \text{i} = 1 }^{\text{n}} w_\text{i} x_\text{i})^2 } \times \begin{pmatrix} { \sum_{\text{i} = 1}^{\text{n}} w_\text{i} x_\text{i}^2 } & { - \sum_{\text{i} = 1}^{\text{n}} w_\text{i} x_\text{i} } \\ { - \sum_{\text{i} = 1}^{\text{n}} w_\text{i} x_\text{i} } & { \sum_{\text{i} = 1}^{\text{n}} w_\text{i} } \\ \end{pmatrix}\end{eqnarray} \) , |
| \( \begin{eqnarray}^\text{t}X \times W \times Y = \begin{pmatrix} { \sum_{\text{i} = 1}^{\text{n}} w_\text{i} y_\text{i} } \\ { \sum_{\text{i} = 1}^{\text{n}} w_\text{i} x_\text{i} y_\text{i} } \\ \end{pmatrix}\end{eqnarray} \) , |
| \( \begin{eqnarray}(^\text{t}X \times W \times X)^{-1} \times ^\text{t}X \times W \times Y = \frac{ 1 }{ \sum_{ \text{i} = 1 }^{\text{n}} w_\text{i} \; \cdot \; \sum_{ \text{i} = 1 }^{\text{n}} w_\text{i} x_\text{i}^2 \; - \; (\sum_{ \text{i} = 1 }^\text{n} w_\text{i} x_\text{i})^2 } \times \begin{pmatrix} { \sum_{\text{i} = 1}^{\text{n}} w_\text{i} x_\text{i}^2 \; \cdot \; \sum_{\text{i} = 1}^{\text{n}} w_\text{i} y_\text{i} \; - \; \sum_{\text{i} = 1}^{\text{n}} w_\text{i} x_\text{i} \; \cdot \; \sum_{\text{i} = 1}^{\text{n}} w_\text{i} x_\text{i} y_\text{i}} \\ { \sum_{\text{i} = 1}^{\text{n}} w_\text{i} \; \cdot \; \sum_{\text{i} = 1}^{\text{n}} w_\text{i} x_\text{i} y_\text{i} \; \; - \sum_{\text{i} = 1}^{\text{n}} w_\text{i} x_\text{i} \; \cdot \; \sum_{\text{i} = 1}^{\text{n}} w_\text{i} y_\text{i}} \\ \end{pmatrix}\end{eqnarray} \) , |
soit :
| \( \begin{eqnarray}a_0 = \frac{ \sum_{\text{i} = 1}^{\text{n}} w_\text{i} y_\text{i} \; \cdot \; \sum_{\text{i} = 1}^{\text{n}} w_\text{i} x_\text{i}^2 \; - \; \sum_{\text{i} = 1}^{\text{n}} w_\text{i} x_\text{i} \;\cdot \; \sum_{\text{i} = 1}^{\text{n}} w_\text{i} x_\text{i} y_\text{i} }{ \sum_{\text{i} = 1}^{\text{n}} w_\text{i} \; \cdot \; \sum_{\text{i} = 1}^{\text{n}} w_\text{i} x_\text{i}^2 \; - \; (\sum_{\text{i} = 1}^{\text{n}} w_\text{i} x_\text{i})^2 }\end{eqnarray} \) , |
| \( \begin{eqnarray}a_1 = \frac{ \sum_{\text{i} = 1}^{\text{n}} w_\text{i} \; \cdot \; \sum_{\text{i} = 1}^{\text{n}} w_\text{i} x_\text{i} y_\text{i} \; - \; \sum_{\text{i} = 1}^{\text{n}} w_\text{i} x_\text{i} \;\cdot \; \sum_{\text{i} = 1}^{\text{n}} w_\text{i} y_\text{i} }{ \sum_{\text{i} = 1}^{\text{n}} w_\text{i} \; \cdot \; \sum_{\text{i} = 1}^{\text{n}} w_\text{i} x_\text{i}^2 \; - \; (\sum_{\text{i} = 1}^{\text{n}} w_\text{i} x_\text{i})^2 }\end{eqnarray} \) . |
Ce qui correspond également aux formules usuelles de la droite des moindres carrés pondérée [1].
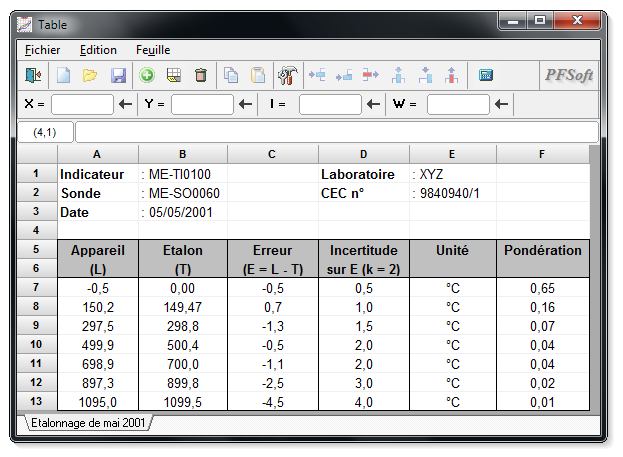
L'étalonnage d'une chaîne de température dotée d'un thermocouple de type K a donné la table d'étalonnage reproduite dans le tableau 1.
| Valeur étalon | Valeur appareil | Erreur | Incertitude |
| 0,00 °C | -0,5 °C | -0,5 °C | 0,5 °C |
| 149,47 °C | 150,2 °C | 0,7 °C | 1,0 °C |
| 298,8 °C | 297,5 °C | -1,3 °C | 1,5 °C |
| 500,4 °C | 499,9 °C | -0,5 °C | 2,0 °C |
| 700,0 °C | 698,9 °C | -1,1 °C | 2,0 °C |
| 899,8 °C | 897,3 °C | -2,5 °C | 3,0 °C |
| 1 099,5 °C | 1 095,0 °C | -4,5 °C | 4,0 °C |
Quel est le meilleur polynôme donnant l'erreur en fonction de la valeur
appareil sur la plage allant de - 0,5 °C à 1 095,0 °C ?
En appliquant la formule (3) on obtient les pondérations wi
reproduites dans le tableau 2.
| Valeur appareil | Erreur | Incertitude | Pondération wi |
| -0,5 °C | -0,5 °C | 0,5 °C | 0,65 |
| 150,2 °C | 0,7 °C | 1,0 °C | 0,16 |
| 297,5 °C | -1,3 °C | 1,5 °C | 0,07 |
| 499,9 °C | -0,5 °C | 2,0 °C | 0,04 |
| 698,9 °C | -1,1 °C | 2,0 °C | 0,04 |
| 897,3 °C | -2,5 °C | 3,0 °C | 0,02 |
| 1 095,0 °C | -4,5 °C | 4,0 °C | 0,01 |
Tout d'abord sur l'interface principale de PolyReg cliquez sur l'icône suivante :
Saisissez ensuite la table d'étalonnage comme suit :
Définissez ensuite la plage des valeurs de X qui seront prises en compte lors des calculs en sélectionnant les cellules du tableau et en cliquant sur l'icône ad hoc comme représenté ci-dessous :
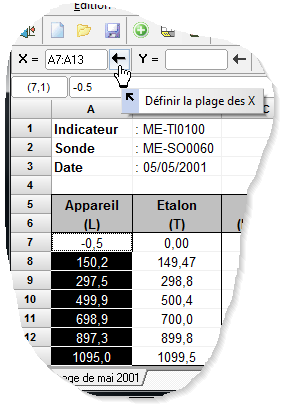
Répétez ensuite l'opération pour les plages des Y, des incertitudes, des pondérations et fermez la feuille.
Lancez ensuite l'assistant de calcul des polynômes en cliquant sur l'icône suivante :
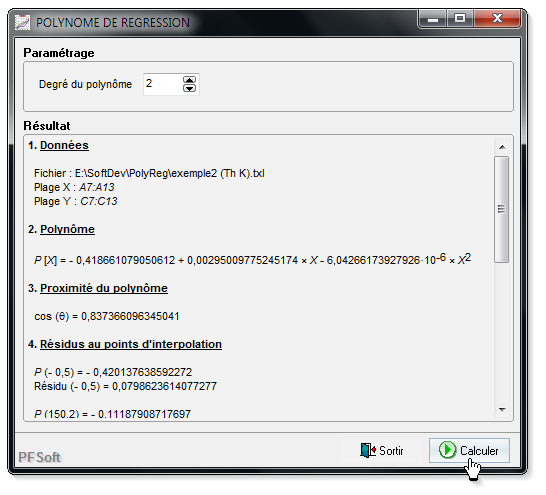
Enfin en sélectionnant le degré du polynôme voulu et en cliquant sur « Calculer… » le polynôme s'affiche automatiquement comme indiqué ci-après.
Fermez à présent le formulaire puis cliquez sur l'icône suivante :
La représentation graphique du polynôme s'affiche alors.
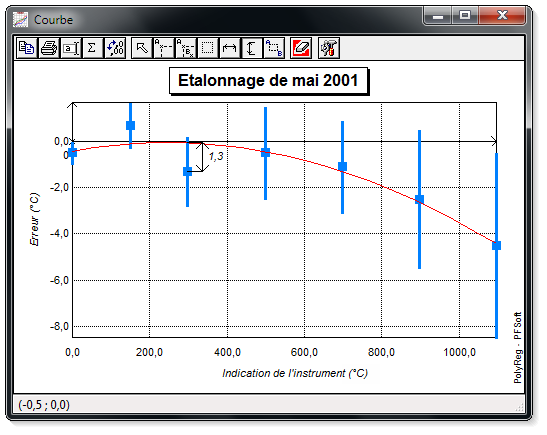
En utilisant les données du tableau 2 avec le logiciel PolyReg et en faisant varier le degré du polynôme entre 1 et 6, on obtient les polynômes donnés dans le tableau 3.
| Degré | Polynôme |
| 1 | \( P[X] = \\ -0,260~445~881~348~811 \\ -0,001~661~700~005~120~21 \times X \) |
| 2 | \( P[X] = \\ -0,418~661~079~050~611 \\ +0,002~950~097~752~451~73 \times X \\ -6,042~661~739~279~26 \times 10^{-6} \times X^2 \) |
| 3 | \( P[X] = \\ -0,438~367~096~842~552 \\ +0,004~503~832~610~367~68 \times X \\ -1,141~423~387~314~53 \times 10^{-5} \times X^2 \\ +3,962~842~847~055~24 \times 10^{-9} \times X^3 \) |
| 4 | \( P[X] = \\ -0,469~274~577~204~221 \\ +0,013~984~577~806~196 \times X \\ -7,334~459~305~439~09 \times 10^{-5} \times X^2 \\ +1,121~598~810~379~47 \times 10^{-7} \times X^3 \\ -5,502~534~204~547~74 \times 10^{-11} \times X^4 \) |
| 5 | \( P[X] = \\ -0,478~223~698~412~436 \\ +0,034~448~062~734~130~1 \times X \\ -0,000~269~648~771~736~598 \times X^2 \\ +6,911~565~376~685 \times 10^{-7} \times X^3 \\ -7,205~720~329~199~88 \times 10^{-10} \times X^4 \\ +2,605~608~842~040~14 \times 10^{-13} \times X^5 \) |
| 6 | \( P[X] = \\ -0,466~793~289~903~802 \\ +0,066~077~305~843~154~4 \times X \\ -0,000~671~003~117~527~796 \times X^2 \\ +2,415~940~582~339~86 \times 10^{-6} \times X^3 \\ -3,992~126~732~558~54 \times 10^{-9} \times X^4 \\ +3,081~345~949~971~13 \times 10^{-12} \times X^5 \\ -9,022~288~897~246~59 \times 10^{-16} \times X^6 \) |
De prime abord, l'on pourrait être tenté de penser que plus le
degré est élevé, meilleur est le polynôme. En fait c'est vrai
mathématiquement mais ça ne l'est pas physiquement : le polynôme est
meilleur aux points des observations, mais la courbe obtenue semble s'éloigner du
modèle physique en présentant des oscillations a priori non nécessaires.
L'utilisation d'un outil graphique tel que PolyReg
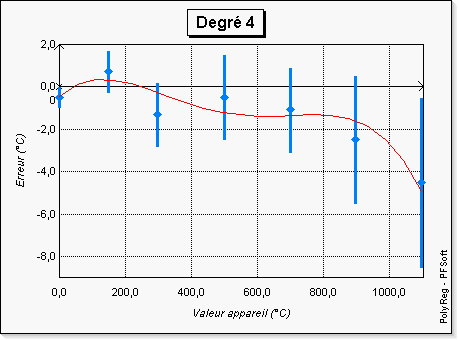
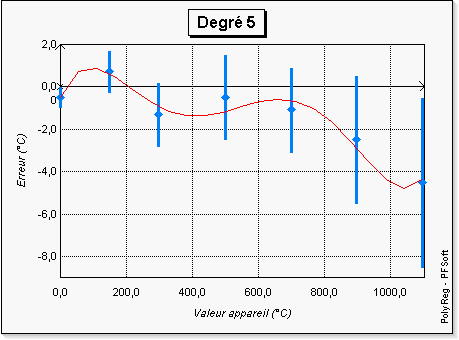
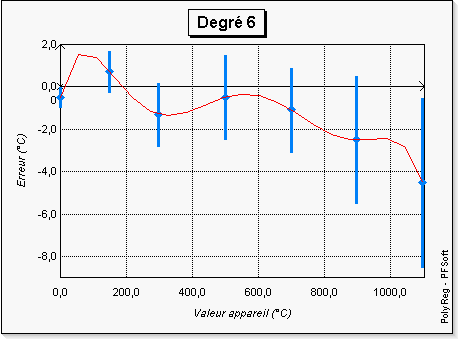
révèle ici tout son intérêt. En effet, sur les figures 3 à
8, l'on a représenté les courbes données par PolyReg
et l'on « voit bien » que pour les degrés supérieurs
à 4 les courbes sont « peu crédibles ».
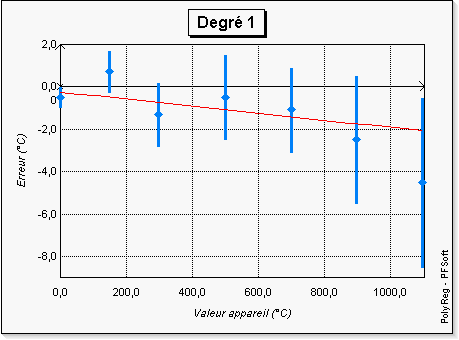
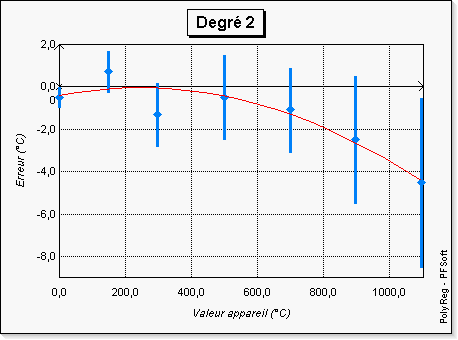
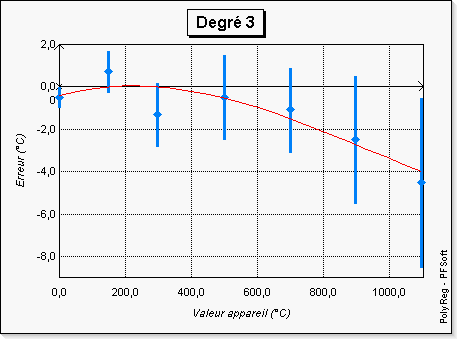
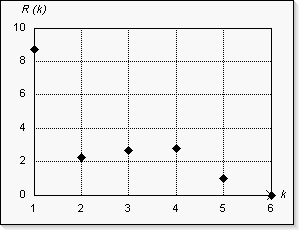
Le tableau 4 donne quant à lui la valeur de \(|\cos \theta| \) ainsi que le résidu absolu maximum et la somme des carrés des résidus. Les valeurs de \( |\cos \theta| \) confirment que plus le degré est élevé, plus le vecteur des observations \( Y \) est proche de sa projection. Les valeurs des sommes des carrés des résidus qui ont été représentées graphiquement sur la figure 9 montrent que si les données suivent une fonction polynomiale, on peut alors penser à l'incertitude de mesure près qu'il s'agit avec une assez bonne approximation d'un polynôme du deuxième degré.
| Degré (k) | \( |\cos \theta| \) | Résidu (Max abs) | \( R(k) \) |
| 1 | 0,694 | 2,420 | 8,689 |
| 2 | 0,837 | 1,224 | 2,233 |
| 3 | 0,843 | 1,296 | 2,664 |
| 4 | 0,902 | 1,022 | 2,772 |
| 5 | 0,972 | 0,665 | 0,969 |
| 6 | 1,000 | 0,000 | 0,000 |
4. Formulaire de calcul en ligne
PolyReg est un logiciel permettant simplement :
Publication associée à ce dossier

|
Télécharger la publication |
| [1] | TAYLOR J., "An introduction to Error Analysis", 2e édition, University Science Books, 1997. |