
 |
Dans le dossier consacré à la détermination des paramètres de l'air humide, nous avons vu que calculer l'humidité relative à partir de la température de rosée n'était pas chose aisée. Cela explique probablement qu'il n'existe apparemment rien dans la littérature apportant des informations concrètes s'agissant de l'humidité relative ainsi calculée. Dans les lignes qui suivent, le lecteur trouvera un calcul d'incertitude sur la détermination de l'humidité relative à partir de la température de rosée, de la température sèche et de la pression atmosphérique. Enfin, les calculs étant un peu lourds à mettre en oeuvre, un formulaire de calcul en ligne a été inclus à la fin de ce dossier.
1. Calcul de l'incertitude
1.1. Rappel de l'équation physique
On a vu dans les dossiers précédents que l'expression donnant l'humidité relative à partir de la température de rosée est de la forme :
| \( \begin{eqnarray}U_\text{w} = 100 \cdot \frac{ f_{w}(P,~\theta_\text{d}) \cdot e_\text{w}~(\theta_\text{d}) }{ f_{w}(P,~\theta_\text{s}) \cdot e_\text{w}~(\theta_\text{s}) }\end{eqnarray} \) , | (1) |
Dans cette expression \( \theta_{d} \) est la température de rosée exprimée en degrés Celsius, \( \theta_{s} \) est la température sèche en degrés Celsius, P est la pression atmosphérique en pascals, Uw est l'humidité relative en pourcents et ew est la pression de vapeur saturante (en pascals) au dessus de l'eau en phase pure définie (d'après [1]) par la relation :
| \( e_{w}(t) = \exp \left[ A \cdot \left(t + 273,15\right)^{2} + B \cdot \left(t + 273,15 \right) + C +\dfrac{D}{t + 273,15} + E \cdot \text{Ln} \left(t + 273,15\right) \right]~\text{,} \) | (2) |
dans laquelle t est la température en degrés Celsius et les coefficients ont les valeurs suivantes :
| \( \left\{\begin{array}{l} A = 1,673~952 \times 10^{-5}~\text{K}^{-2} \\ B = -2,711~193 \times 10^{-2}~\text{K}^{-1} \\ C = 21,240~964~2 \\ D = -6~096,938~5~\text{K} \\ E = 2,433~502 \end{array} \right. \) |
Dans l'expression (1), fw est le facteur d'augmentation défini (d'après [1]) par la relation :
| \( f_{w}(P,~t) = \exp \left[ \alpha \cdot \left( 1 - \dfrac{e_{W}(t)}{P} \right) + \beta \cdot \left( \dfrac{P}{e_{W}(t)} - 1 \right) \right]~\text{,} \) | (3) |
dans laquelle t est la température en degrés Celsius et P la pression en pascals avec :
| \( \alpha = \displaystyle\sum\limits_{i~=~0}^{3} A_{i} \cdot t^{i}~\text{,} \) | (4) |
| \( \beta = \exp \left[ \displaystyle\sum\limits_{i~=~0}^{3} B_{i} \cdot t^{i} \right]~\text{,} \) | (5) |
et les coefficients ayant les valeurs suivantes :
| \( \left\{\begin{array}{l} A_{0} = 3,536~24 \times 10^{-4} \\ A_{1} = 2,932~28 \times 10^{-5}~\text{°C}^{-1} \\ A_{2} = 2,614~74 \times 10^{-7}~\text{°C}^{-2} \\ A_{3} = 8,575~38 \times 10^{-9}~\text{°C}^{-3} \\ B_{0} = -10,758~8 \\ B_{1} = 6,325~29 \times 10^{-2}~\text{°C}^{-1} \\ B_{2} = -2,535~91 \times 10^{-4}~\text{°C}^{-2} \\ B_{3} = 6,337~84 \times 10^{-7}~\text{°C}^{-3} \end{array} \right. \) |
1.2. Modèle de la mesure
L'équation physique (1) doit être complétée pour prendre en compte le fait que fw et ew sont connus grâce à des modèles approchés. Le modèle de la mesure est donc :
| \( \begin{eqnarray}U_\text{w} = 100 \cdot \dfrac{ \left[ f_{w}(p,~\theta_\text{d}) + C_\text{fwd} \right] \cdot \left[ e_\text{w}~(\theta_\text{d}) + C_\text{ewd} \right] }{ \left[ f_{w}(p,~\theta_\text{s}) + C_\text{fws} \right] \cdot \left[ e_\text{w}~(\theta_\text{s}) + C_\text{ews} \right] }\end{eqnarray}~\text{,} \) | (6) |
avec :
Dans la pratique toutes ces corrections sont de valeur nulle en moyenne mais pas leur incertitudes.
1.3. Linéarité du modèle
Avant d'appliquer la loi de propagation des variances, il est nécessaire de s'assurer de la linéarité du modèle employé. Les graphiques ci-dessous (figures 1 à 7) incitent à penser que localement la linéarité du modèle est suffisante pour se limiter au premier ordre lors du développement de Uw. Cette hypothèse sera confirmée par la suite par simulation de Monte-Carlo (cf. 3.).
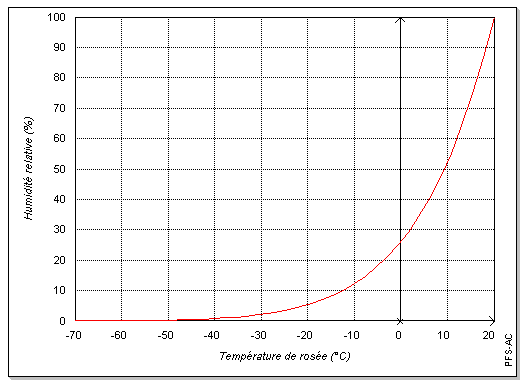
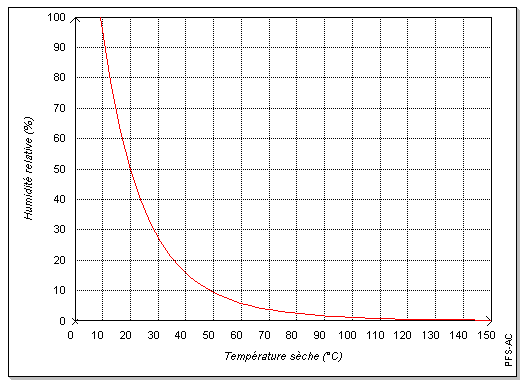
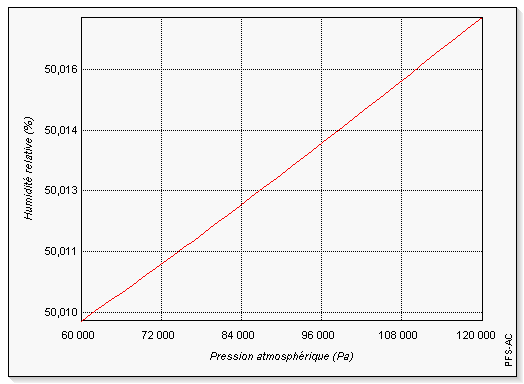
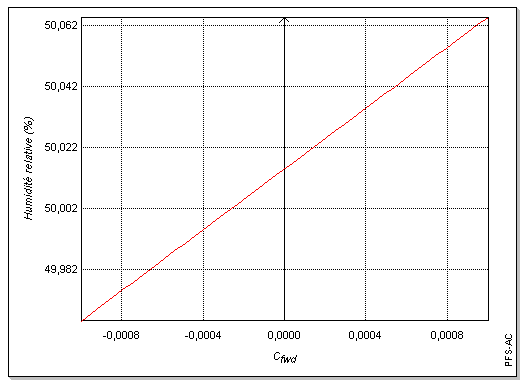
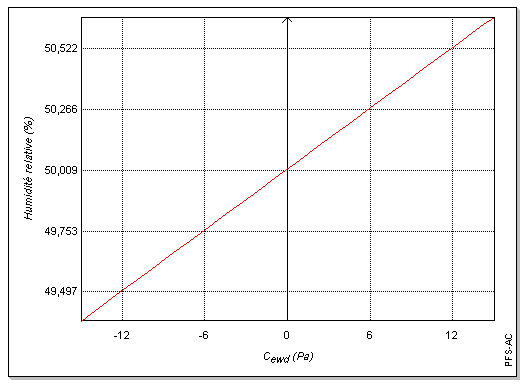
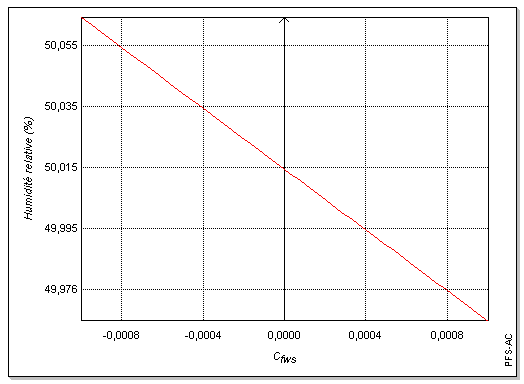
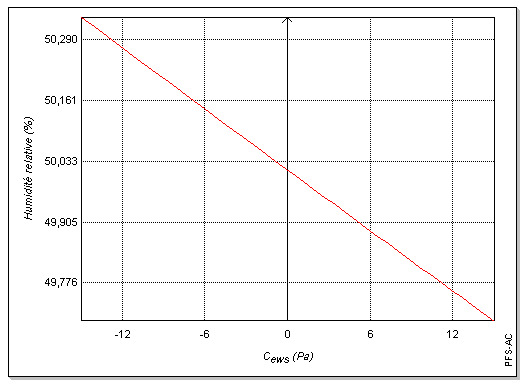
1.4. Propagation des variances
La loi de propagation des variances appliquée au modèle (6) s'écrit :
| \( u^{2}(U_{\text{w}}) = \left( \dfrac{\partial U_{\text{w}} }{ \partial \theta_{\text{d}}} \right)^{2} \cdot u^{2}(\theta_{\text{d}}) + \left( \dfrac{\partial U_{\text{w}} }{ \partial \theta_{\text{s}}} \right)^{2} \cdot u^{2}(\theta_{\text{s}}) + \left( \dfrac{\partial U_{\text{w}} }{ \partial p } \right)^{2} \cdot u^{2}(p) + \left( \dfrac{\partial U_{\text{w}} }{ \partial C_{\text{fwd}} } \right)^{2} \cdot u^{2}(C_{\text{fwd}}) \)
\( \quad \quad \quad + \left( \dfrac{\partial U_{\text{w}} }{ \partial C_{\text{ewd}} } \right)^{2} \cdot u^{2}(C_{\text{ewd}}) + \left( \dfrac{\partial U_{\text{w}} }{ \partial C_{\text{fws}} } \right)^{2} \cdot u^{2}(C_{\text{fws}}) + \left( \dfrac{\partial U_{\text{w}} }{ \partial C_{\text{ews}} } \right)^{2} \cdot u^{2}(C_{\text{ews}}) \) , |
(7) |
Note : dans les calculs qui suivent Cfws est considéré comme une variable aléatoire d'éspérance mathématique nulle et de distribution uniforme. La demie étendue de cette loi est majorée sur la plage de définition de P et θs, ce qui permet alors de considérer la variable Cfws comme non corrélée avec les autres variables. On applique le même raisonnement à Cfwd, ews et ewd.
1.5. Calcul des coefficients de sensibilité
1.5.1 Dérivées des modèles de base
Les dérivées de Uw font apparaître la dérivée de la pression de vapeur saturante ew par rapport à la température et les dérivées partielles du facteur d'augmentation par rapport à la température et par rapport à la pression.
1.5.1.1 Pression de vapeur saturante au dessus de l'eau en phase pure
| \( \dfrac{ \mathrm{d}e_{\text{w}} }{ \mathrm{d}t }(t) = \left[ 2 \cdot A \cdot \left(t + 273,15\right) + B - \dfrac{D}{\left(t + 273,15\right)^{2}} + \dfrac{E}{t + 273,15}\right] \cdot e_{\text{w}}(t)\quad\text{,} \) | (8) |
avec t la température en degrés Celsius et :
| \( \left\{\begin{array}{l} A = 1,673~952 \times 10^{-5}~\text{K}^{-2} \\ B = -2,711~193 \times 10^{-2}~\text{K}^{-1} \\ C = 21,240~964~2 \\ D = -6~096,938~5~\text{K} \\ E = 2,433~502 \end{array} \right. \) |
1.5.1.2 Facteur d'augmentation
La dérivée par rapport à la température s'écrit :
| \( \dfrac{ \partial f_{\text{w}} }{ \partial t}(p,~t) = \left[ \dfrac{ \mathrm{d} \alpha }{ \mathrm{d} t }(t) \cdot \left( 1 - \dfrac{ e_{\text{w}}(t) }{ p } \right) - \dfrac{ \alpha (t)}{ p } \cdot \dfrac{ \mathrm{d} e_{\text{w}} }{ \mathrm{d} t }(t) \\ \quad \quad + \dfrac{ \mathrm{d} \beta }{ \mathrm{d} t }(t) \cdot \left( \dfrac{ p }{ e_{\text{w}} (t) } - 1 \right) - \dfrac{ p \cdot \beta (t) }{ e^{2}_{\text{w}} (t) } \cdot \dfrac{ \mathrm{d} e_{\text{w}} }{ \mathrm{d} t }(t) \right] \cdot f_{\text{w}}(p,~t) \) | (9) |
avec t la température en degrés Celsius et les fonctions
α et β
définies dans les équations (4) et (5).
Les dérivées de α et β sont :
| \( \dfrac{ \mathrm{d} \alpha }{ \mathrm{d} t }(t) = \displaystyle\sum\limits_{i~=~1}^{3} i \cdot A_{\text{i}} \cdot t^{\text{i} - 1}~\text{,} \) | (10) |
| \( \dfrac{ \mathrm{d} \beta }{ \mathrm{d} t }(t) = \beta (t) \cdot \displaystyle\sum\limits_{i~=~1}^{3} i \cdot B_{\text{i}} \cdot t^{\text{i} - 1}~\text{.} \) | (11) |
Et enfin, la dérivée par rapport à la pression s'écrit :
| \( \dfrac{ \partial f_{\text{w}} }{ \partial p} = \left[ \dfrac{ \alpha (t) \cdot e_{\text{w}} (t) }{ p^{2} } + \dfrac{ \beta (t) }{ e_{\text{w}} (t) } \right] \cdot f_{\text{w}}(p,~t)~\text{.} \) | (12) |
1.5.2 Dérivées du modèle
En remarquant que Cews = Cewd = 0 et Cfws = Cfwd = 0, il vient les dérivées suivantes :
| \( \dfrac{ \partial U_{\text{w}} }{ \partial \theta_{\text{d}} }(p,~\theta_{\text{s}},~\theta_{\text{d}}) = \dfrac{ 100 }{ f_{\text{w}}(p,~\theta_{\text{s}}) \cdot e_{\text{w}}(\theta_{\text{s}}) } \cdot \left[ \dfrac{ \partial f_{\text{w}} }{ \partial t}(p,~\theta_{\text{d}}) \cdot e_{\text{w}}(\theta_{\text{d}}) + \dfrac{ \mathrm{d} e_{\text{w}} }{ \mathrm{d} t }(\theta_{\text{d}}) \cdot f_{\text{w}}(p,~\theta_{\text{d}} \right]~\text{,} \) | (13) |
| \( \dfrac{ \partial U_{\text{w}} }{ \partial \theta_{\text{s}} }(p,~\theta_{\text{s}},~\theta_{\text{d}}) = -U_{\text{w}}(p,~\theta_{\text{s}},~\theta_{\text{d}}) \cdot \dfrac{ \dfrac{ \partial f_{\text{w}} }{ \partial t}(p,~\theta_{\text{s}}) \cdot e_{\text{w}}(\theta_{\text{s}}) + \dfrac{ \mathrm{d} e_{\text{w}} }{ \mathrm{d} t}(\theta_{\text{s}}) \cdot f_{\text{w}}(p,~\theta_{\text{s}}) }{ f_{\text{w}}(p,~\theta_{\text{s}}) \cdot e_{\text{w}}(\theta_{\text{s}}) }~\text{,} \) | (14) |
| \( \dfrac{ \partial U_{\text{w}} }{ \partial p }(p,~\theta_{\text{s}},~\theta_{\text{d}}) = U_{\text{w}}(p,~\theta_{\text{s}},~\theta_{\text{d}}) \cdot \dfrac{ \dfrac{ \partial f_{\text{w}} }{ \partial t }(p,~\theta_{\text{d}}) \cdot f_{\text{w}}(p,~\theta_{\text{s}}) - \dfrac{ \partial f_{\text{w}} }{ \partial p }(p,~\theta_{\text{s}}) \cdot f_{\text{w}}(p,~\theta_{\text{d}}) }{ f_{\text{w}}(p,~\theta_{\text{s}}) \cdot f_{\text{w}}(p,~\theta_{\text{d}}) }~\text{,} \) | (15) |
| \( \dfrac{ \partial U_{\text{w}} }{ \partial C_{\text{fwd}} }(p,~\theta_{\text{s}},~\theta_{\text{d}}) = \dfrac{U_{\text{w}}(p,~\theta_{\text{s}},~\theta_{\text{d}}) }{ f_{\text{w}}(p,~\theta_{\text{d}}) }~\text{,} \) | (16) |
| \( \dfrac{ \partial U_{\text{w}} }{ \partial C_{\text{ewd}} }(p,~\theta_{\text{s}},~\theta_{\text{d}}) = \dfrac{U_{\text{w}}(p,~\theta_{\text{s}},~\theta_{\text{d}}) }{ e_{\text{w}}( \theta_{\text{d}}) }~\text{,} \) | (17) |
| \( \dfrac{ \partial U_{\text{w}} }{ \partial C_{\text{fws}} }(p,~\theta_{\text{s}},~\theta_{\text{d}}) = \dfrac{-U_{\text{w}}(p,~\theta_{\text{s}},~\theta_{\text{d}}) }{ f_{\text{w}}(p,~\theta_{\text{s}}) }~\text{,} \) | (18) |
| \( \dfrac{ \partial U_{\text{w}} }{ \partial C_{\text{ews}} }(p,~\theta_{\text{s}},~\theta_{\text{d}}) = \dfrac{-U_{\text{w}}(p,~\theta_{\text{s}},~\theta_{\text{d}}) }{ e_{\text{w}}(\theta_{\text{s}}) }~\text{.} \) | (19) |
1.6. Composantes d'incertitudes
Les incertitudes élémentaires u(θd) sur la température de rosée, u(θs) sur la température sèche et u(p) sur la pression atmosphérique sont des données issues des mesures effectuées. Il reste à calculer les composantes dues à la modélisation de fw, c'est-à-dire u(Cfws) et u(Cfwd) ainsi que les composantes dues à la modélisation de ew, c'est-à-dire u(Cews) et u(Cewd).
En ce qui concerne la composante d'incertitude due à la modélisation de fw, c'est-à-dire u(Cfw) ainsi que la composante due à la modélisation de ew, c'est-à-dire u(Cew) les valeurs données dans les paragraphes suivants sont recommandées.
Incertitude due à la modélisation de fw : u (Cfw)
D'après la référence
[1],
l'incertitude sur la modélisation de fw est de 0,08 % en valeur
relative. En remarquant que fw < 1,1 on a alors une erreur
de modélisation inférieure à 0,000 88 d'où
l'incertitude type :
\( u(C_{\text{fw}}) = \dfrac{0,000~88}{ \sqrt{3} } \approx 0,000~51~\text{.} \)
On retiendra donc :
\( u(C_{\text{fw}}) = 0,000~51~\text{.} \)
Incertitude due à la modélisation de ew : u (Cew)
D'après la référence
[1],
l'incertitude sur la modélisation de ew est de 0,01 % en valeur
relative. En remarquant que ew est une fonction croissante il suffit
de limiter le domaine d'utilisation en température et de considérer la
valeur maximale de la pression ew. D'où l'incertitude
type :
\( u(C_{\text{ew}}) = 1 \times 10^{-4} \dfrac{ e_{\text{wmax}} }{ \sqrt{3} }~\text{Pa .} \)
Une série de valeurs de u (Cew) sont proposées
dans le tableau 1 (dans ce tableau θm
représente la température sèche maximale possible lors de l'utilisation du convertisseur).
| θm en °C | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| u (Cew) en Pa | 0,14 | 0,25 | 0,43 | 0,72 | 1,15 | 1,81 | 2,74 | 4,06 | 5,85 |
2. Calcul en ligne
Remarque : on observera qu'en saisissant des incertitudes types nulles pour la température de rosée, la température sèche et la pression atmosphérique on obtient alors l'incertitude type due uniquement à la formule de conversion. Par exemple pour une température sèche de 20,00 °C, une température de rosée de 9,28 °C et une pression atmosphérique de 101 325 Pa l'incertitude élargir due à la formule de conversion est 0,08 % (k = 2). En conservant à l'esprit que les incertitudes d'étalonnage au meilleur niveau sont généralement de quelques dixièmes de pourcents, ceci prouve qu'il ne faut pas négliger l'incertitude sur les modélisations.
3. Validation du calcul d'incertitude par simulation de Monte-Carlo
Si la méthode de propagation des variances recommandée par le GUM [2] est acquise, il n'en demeure pas moins que son application à un modèle donné suppose quelques hypothèses, notamment de linéarité du modèle. La méthode de propagation des des distributions par simulation de Monte-Carlo [3] permet de calculer l'incertitude au moyen d'une autre méthode et de s'assurer que la méthode du GUM s'applique [4]. Le calcul de l'incertitude par simulation de Monte-Carlo a été effectué au moyen du logiciel MC-Ed [4].
En considérant les données suivantes :
| θs | = | 20,00 °C ; | |
| u (θs) | = | 0,05 °C ; | |
| θd | = | 9,28 °C ; | |
| u (θd) | = | 0,05 °C ; | |
| Patm | = | 101 325 Pa ; | |
| u (Patm) | = | 10 Pa ; | |
| u (Cfw) | = | 0,000 51 ; | |
| u (Cew) | = | 0,25 Pa, |
le calcul effectué au moyen du formulaire du paragraphe 2 donne avec un coefficient d'élargissement k = 2 :
| Uw = (50,01 ± 0,46) %, i.e. Uw ∈ [49,55 % ; 50,47 %]. |
Le même calcul effectué au moyen de MC-Ed [4] donne pour un échantillon de 100 000 valeurs, l'intervalle élargi à 95 % suivant :
| Uw ∈ [49,55 % ; 50,46 %]. |
La statistique par classes obtenue avec MC-Ed représentant la moyenne et l'intervalle élargi à 95 % est représenté sur la figure 8.
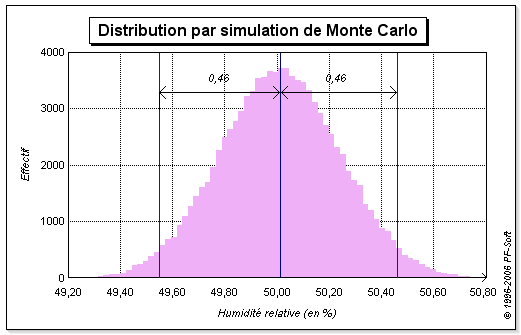
Les calculs effectués en utilisant la loi de propagation des variances et en utilisant la simulation de Monte-Carlo étant cohérents, l'application du GUM au modèle (6) est validée.
Le fichier contenant ce calcul, à utiliser avec MC-Ed, est disponible dans le lien suivant (décompresser l'archive dans le répertoire de MC-Ed) :
 |
Calcul de l'incertitude avec MC-Ed |
Remarque : les échantillons occupant un espace mémoire important, ceux-ci ne sont pas inclus dans l'archive. Vous devrez les générer sur votre machine.
| [1] | "A guide to the measurement of humidity", National Physical Laboratory, Teddington. |
| [2] | JCGM, « évaluation des données de mesure - Guide pour l'expression de l'incertitude de mesure », BIPM, JCGM 100:2008 (version française), septembre 2008, www.bipm.org. |
| [3] | JCGM, "Evaluation of measurement data - Supplement 1 to the "Guide to the expression of uncertainty in measurement" - Propagation of distributions using a Monte-Carlo method", BIPM, JCGM 101:2008, 2008, www.bipm.org. |
| [4] | PLATEL F., « Mise en pratique de la méthode de Monte-Carlo - Projet Monte-Carlo Editor (MC-Ed) », MetGen, Dossier métrologie 25. |