
 |
1. Utilité de la méthode de Monte-Carlo pour calculer des incertitudes
Il existe aujourd'hui deux approches définies par le Guide to the expression of uncertainty in measurement (en abrégé GUM) [1, 2] pour calculer des incertitudes :
La première méthode est souvent appelée « GUM analytique » par opposition à la seconde qui est une méthode essentiellement numérique.
Remarque : il existe en fait une troisième méthode reposant sur des comparaisons interlaboratoire [3]. Cette méthode est motivée par la difficulté dans certains cas à trouver le modèle de la mesure. Ceci étant, elle souffre de deux handicaps majeurs : elle n'est pas construite pour assurer un continuum de traçabilité (la traçabilité intervient au travers d'une correction ajoutée en fin de calcul, ce qui est un constat d'échec) ; elle nécessite d'organiser des comparaisons inter laboratoires (ce qui est très lourd à organiser, bien souvent plus lourd que de passer un peu de temps pour construire le modèle de la mesure...). Ajoutons que le temps passé pour construire le modèle de la mesure est un coût fixe. Autrement dit, dans le cas de l'approche GUM une modification des paramètres de la mesure se traduit le plus souvent par une modification de valeurs affectées à des variables. Dans le cas d'une approche 5725, il faut procéder à des nouvelles campagnes de comparaisons interlaboratoire : ce qui d'un point de vue économique devient rapidement désastreux. Pour ces raisons, l'approche 5725 est à éviter.
Jusqu'à présent dans l'industrie les incertitudes ont essentiellement été calculées par la méthode du GUM en propageant des variances. Cette méthode largement reconnue ayant fait l'objet de nombreuses publications, il pourrait être légitime de s'interroger sur l'utilité d'introduire une nouvelle méthode. En réponse, cette méthode pose un certain nombre d'hypothèses - en particulier sur la linéarité du modèle (cf. démonstrations) - qui font que son application peut être erronée pour un calcul d'incertitude donné. Afin de pouvoir valider l'application du GUM à un calcul d'incertitude, le moyen le plus simple est de le comparer à un calcul effectué par une autre méthode. La méthode de Monte-Carlo est tout à fait indiquée pour effectuer cette comparaison puisqu'elle ne pose pas d'hypothèses sur le modèle de la mesure.
A contrario on pourrait maintenant s'interroger sur l'utilité de conserver la méthode du GUM si la méthode de Monte-Carlo ne présente pas les inconvénients du GUM. En réponse, la mise en oeuvre de la méthode de Monte-Carlo (détaillée dans les références [4], [5] et [6]) est extrêmement lourde en calculs et nécessite un logiciel spécifique. Pour cette raison, il est préférable de conserver autant que possible la méthode du GUM.
De nombreux référentiels normatifs (tels que la 17025 [7]) utilisés dans le cadre des systèmes qualité des entreprises exigent que les méthodes soient validées. Afin d'être en conformité avec ces exigences, le plus simple est de concevoir dans un premier temps le calcul d'incertitudes par la méthode du GUM. Puis dans un second temps de le valider par la méthode de Monte-Carlo. Cela étant fait, l'application de la méthode du GUM sera validée pour le modèle de la mesure considéré ; il sera alors possible par la suite d'utiliser uniquement la méthode du GUM. En conclusion, la méthode de Monte-Carlo est un outil, nécessaire, à utiliser au moment de la conception des calculs d'incertitudes, en complément de la méthode du GUM.
La mise en oeuvre de la Méthode de Monte-Carlo présentée dans les références [4], [5] et [6] conduit à utiliser des logiciels fonctionnant en mode ligne de commande (« Pack Monte-Carlo »). Cette approche modulaire autorise une grande souplesse et permet de travailler avec des échantillons de taille élevées (plusieurs millions de valeurs). En revanche l'ergonomie n'est pas satisfaisante. Pour cette raison le lecteur trouvera dans les lignes qui suivent le logiciel MC-Ed (Monte-Carlo Editor) utilisant la souplesse de l'interface Windows tout en conservant la puissance de calcul du Pack Monte-Carlo.
2. Le logiciel MC-Ed : principales caractéristiques et fonctionnalités
Le logiciel MC-Ed est avant tout une interface graphique qui permet de piloter les logiciels du Pack Monte-Carlo en utilisant l'environnement Windows. Ses principales caractéristiques et fonctionnalités sont :
Une interface intuitive...
|
L'ensemble des grandeurs intervenant dans le modèle de la mesure est présenté de façon synthétique et visuelle dans un tableau. Le logiciel permet de jongler entre quatre écrans correspondants aux quatre grandes étapes du calcul d'incertitudes :
L'utilisation d'onglets imbriqués permet d'accéder sur les différents écrans à chacune des grandeurs sans recourir à de nombreuses boites de dialogue. |
Fig. 1. - Interface de MC-Ed.
(Cliquez sur l´image pour l´agrandir) |
Définition des grandeurs d'entrée au moyen d'assistants...
|
Fig. 2. - Définition de la loi des grandeurs d'entrée.
(Cliquez sur l´image pour l´agrandir) |
Après avoir saisi le modèle de la mesure au moyen d'une équation PFS-AC
[8],
le logiciel invite l'utilisateur à définir les lois des grandeurs d'entrée.
|
Réaliser différents calculs sur chacune des grandeurs d'entrée...
|
Pour chaque grandeur d'entrée et pour la grandeur de sortie, il est possible de calculer la
moyenne, l'écart type ainsi qu'un intervalle élargi.
|
Fig. 3. - Calculs sur les échantillons.
(Cliquez sur l´image pour l´agrandir) |
Visualiser les résultats pour chaque grandeur...
|
Fig. 4. - Exemple de représentation graphique.
(Cliquez sur l´image pour l´agrandir) |
Pour chaque grandeur d'entrée et la grandeur de sortie MC-Ed permet de tracer :
Les différentes courbes peuvent être annotées, les légendes , les résolutions et les échelles peuvent être modifiées. Les graphiques peuvent être exportés sous la forme d'images par copier/coller dans la plupart des applications de bureautique. |
Sauvegarder l'ensemble d'un calcul (y compris les échantillons)...
MC-Ed permet de sauvegarder l'ensemble des données dans un format compressé. Cette fonctionnalité permet d'assurer la traçabilité documentaire d'une validation effectuée dans le cadre d'un système qualité [7].
Faire évoluer les modules de calculs (pour utilisateurs expérimentés)...
|
MC-Ed permet de modifier le paramétrage des logiciels du Pack Monte-Carlo, voire de piloter vos
propres logiciels de calcul pouvant se substituer ou compléter les logiciels du Pack Monte-Carlo.
|
Fig. 5. - Paramétrage du Pack Monte-Carlo.
(Cliquez sur l´image pour l´agrandir) |
4. Exemple : étalonnage d'une micropipette
Les micropipettes sont étalonnées par méthode gravimétrique en utilisant l'eau, dont on connait la masse volumique, comme fluide de référence [9]. Cette méthode consiste à déverser le contenu de la pipette à étalonner dans un récipient posé sur une balance et à mesurer la variation de masse. Le volume délivré par la micropipette est déterminé par la relation :
| \( \begin{eqnarray}V_{20} = M \cdot \frac{ 1 }{ \rho_{\text{W}} - \rho_{\text{A}} } \cdot \left( 1 - \frac{\rho_{\text{A}}}{\rho_{\text{B}}} \right) \cdot \bigl[ 1 - \gamma \cdot (t - 20) \bigr] \end{eqnarray} \) , | (1) |
dans laquelle :
| \( V_{20} \) | : est le volume à la température de 20 °C délivré par la pipette (en µl) ; |
| \( M \) | : est la variation de masse indiquée par la balance (en mg) ; |
| \( t \) | : est la température de l'eau pendant la mesure (en °C) ; |
| \( \rho_{\text{W}} \) | : est la masse volumique de l'eau (en mg/µl) ; |
| \( \rho_{\text{A}} \) | : est la masse volumique de l'air pendant la mesure (en mg/µl) ; |
| \( \rho_{\text{B}} \) | : est la masse volumique des masses utilisées pour étalonner la balance (en mg/µl) ; |
| \( \gamma \) | : est le coefficient de dilatation thermique de la micropipette (en l/K). Celui-ci est généralement donné par le constructeur. |
Dans la réalité, la masse \( M \) que l'on mesure est affectée d'une erreur due à la résolution de la balance (\( \delta m_{\text{res}} \)) et d'une erreur due à l'étalonnage de la balance (\( \delta m_{\text{étal}} \)). De même la température est affectée d'une erreur due à l'étalonnage du thermomètre (\( \delta t_{\text{étal}} \)). La prise en compte de ces erreurs permet de déduire le modèle de la mesure :
| \( \begin{eqnarray}V_{20} = \left( M + \delta m_{\text{res}} + \delta m_{\text{étal}} \right) \cdot \frac{ 1 }{ \rho_{\text{W}} - \rho_{\text{A}} } \cdot \left( 1 - \frac{\rho_{\text{A}}}{\rho_{\text{B}}} \right) \cdot \bigl[ 1 - \gamma \cdot (t + \delta t_{\text{étal}} - 20) \bigr] \end{eqnarray} \) . | (2) |
Cette équation a été programmée dans PFS-AC [8]. Elle est téléchargeable dans le lien suivant (décompresser l'archive au format zip pour utiliser le fichier modele_pipette.fct).
Dans le cadre de cet exemple, nous utiliserons les données de la référence [10] reproduites dans le tableau 1.
| Variable | Estimation | Loi | Incertitude type |
| \( M \) | \( 5,033~\text{µg} \) | Normale | \( 8,8 \times 10^{-3}~\text {µg} \) |
| \( t \) | \( 19,5~\text{°C} \) | Rectangle | \( 0 \text{°C} \) |
| \( \rho_{\text{W}} \) | \( 0,998~3~\text{µg/µl} \) | Rectangle | \( 1,16 \times 10^{-5}~\text{µg/µl} \) |
| \( \rho_{\text{A}} \) | \( 1,2 \times 10^{-3}~\text{µg/µl} \) | Rectangle | \( 2,89 \times 10^{-7}~\text{µg/µl} \) |
| \( \rho_{\text{B}} \) | \( 7,96~\text{µg/µl} \) | Rectangle | \( 0,0346~\text{µg/µl} \) |
| \( \gamma \) | \( 2,40 \times 10^{-4}~\text{l/K} \) | Rectangle | \( 2,89 \times 10^{-6}~\text{l/K} \) |
| \( \delta m_{\text{res}} \) | \( 0~\text{µg} \) | Rectangle | \( 0,001~\text{µg} \) |
| \( \delta m_{\text{étal}} \) | \( 0~\text{µg} \) | Normale | \( 0,005~\text{µg} \) |
| \( \delta t_{\text{étal}} \) | \( 0~\text{°C} \) | Normale | \( 0,05~\text{°C} \) |
Tout d'abord, les coefficients de sensibilité ont été calculé en utilisant la fonction dérivation de PFS-AC [8] appliquée à chacune des grandeurs d'entrée du modèle. Ces valeurs sont reproduites dans le tableau 2.
| Variable | Coefficient de sensibilité |
| \( M \) | \( 1,002~9 \) |
| \( t \) | \( -1,211~3 \times 10^{-3} \) |
| \( \rho_{\text{W}} \) | \( -5,062~2 \) |
| \( \rho_{\text{A}} \) | \( 4,428~0 \) |
| \( \rho_{\text{B}} \) | \( 9,560~8 \times 10^{-5} \) |
| \( \gamma \) | \( 2,523~4 \) |
| \( \delta m_{\text{res}} \) | \( 1,002~9 \) |
| \( \delta m_{\text{étal}} \) | \( 1,002~9 \) |
| \( \delta t_{\text{étal}} \) | \( -1,211~3 \times 10^{-3} \) |
Les données des tableaux 1 et 2 ont été utilisées pour effectuer le calcul d'incertitude en utilisant la loi de propagation des variances (méthode du GUM) avec le logiciel Gumy [11]. Le fichier de calcul est téléchargeable dans le lien suivant (décompresser l'archive au format zip pour utiliser le fichier etalonnage_pipette.gmy).
Le détail des calculs produits par Gumy est reporté dans le tableau 3. Le volume calculé par cette méthode avec un facteur d'élargissement \( k = 2 \) vaut :
| \( V_{20} = (5,047 ± 0,021)~µl \) | (3) |
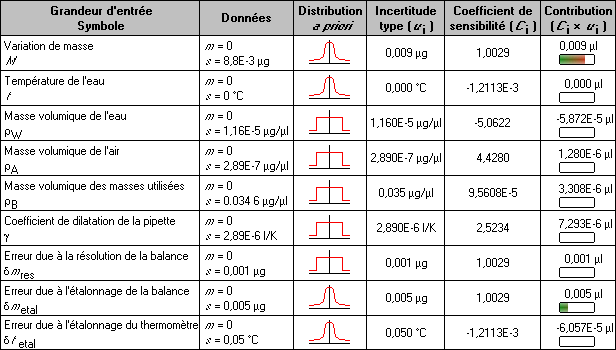
On remarque au passage que cette méthode présente l'avantage de fournir les principales composantes d'incertitude. En effet, d'après le tableau 3 il apparaît clairement que la principale cause d'incertitude est la mesure de la variation de masse (répétabilité) et dans une moindre mesure l'étalonnage de la balance. Cette information n'est pas accessible simplement par la méthode de Monte-Carlo.
4.2. Propagation des distributions avec MC-Ed
Les lois rectangle étant définies par des demi étendues sur MC-Ed, il est nécessaire de transformer les données du tableau 1 pour les rendre exploitables (les formules de conversion sont rappelées dans l'assistant de saisie des lois sur MC-Ed). Les données transformées sont fournies dans le tableau 4.
| Variable | Estimation | Loi | Incertitude type | Demi étendue* |
| \( M \) | \( 5,033~\text{µg} \) | Normale | \( 8,8 \times 10^{-3}~\text{µg} \) | / |
| \( t \) | \( 19,5~\text{°C} \) | Rectangle | / | \( 0~\text{°C} \) |
| \( \rho_{\text{W}} \) | \( 0,998~3~\text{µg/µl} \) | Rectangle | / | \( 2,01 \times 10^{-5}~\text{µg/µl} \) |
| \( \rho_{\text{A}} \) | \( 1,2 \times 10^{-3}~\text{µg/µl} \) | Rectangle | / | \( 5,01 \times 10^{-7}~\text{µg/µl} \) |
| \( \rho_{\text{B}} \) | \( 7,96~\text{µg/µl} \) | Rectangle | / | \( 0,059~9~\text{µg/µl} \) |
| \( \gamma \) | \( 2,40 \times 10^{-4}~\text{l/K} \) | Rectangle | / | \( 5,01 \times 10^{-6}~\text{l/K} \) |
| \( \delta m_{\text{res}} \) | \( 0 \) | Rectangle | / | \( 0,001~73~\text{µg} \) |
| \( \delta m_{\text{étal}} \) | \( 0 \) | Normale | \( 0,005~\text{µg} \) | / |
| \( \delta t_{\text{étal}} \) | \( 0 \) | Normale | \( 0,05~\text{°C} \) | / |
Le calcul effectué avec MC-Ed donne pour un échantillon de 100 000 valeurs :
| \( \left\{ \begin{array}{l} \text{Moyenne}~V_{20} = 5,047~\text{µl}~; \\ \text{Ecart type} = 0,010~2~\text{µl}~; \\ \text{Intervalle élargi :}~\bigl[5,026~\text{µl}~;~5,067~\text{µl}\bigr]. \end{array} \right. \) . | (4) |
La statistique par classes avec la valeur moyenne et l'intervalle élargi obtenue par MC-Ed est représentée sur la figure 6.
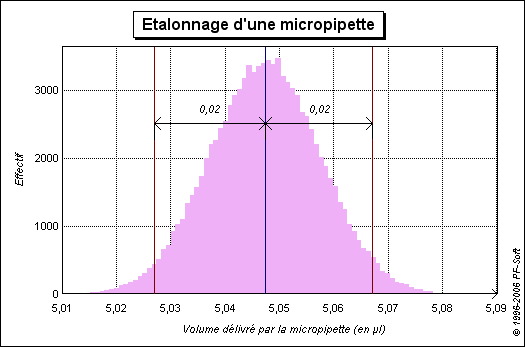
Le tableau 5 présente les résultats obtenus par la méthode du GUM (3) et par la méthode de Monte-Carlo (4). Les résultats sont très voisins, ce qui permet de conclure que l'application de la loi de propagation des variances (méthode GUM) est validée pour le modèle de la mesure (localement au point de mesure considéré).
| Grandeur | Méthode GUM | Méthode de Monte-Carlo |
| \( V_{20} \) | \( 5,047~\text{µl} \) | \( 5,047~\text{µl} \) |
| Ecart type | \( 0,010~3~\text{µl} \) | \( 0,010~2~\text{µl} \) |
| Intervalle élargi (en µl) |
\( [5,026~;~5,068] \) (\( k = 2\)) |
\( [5,026~;~5,067] \) (à 95 %) |
 |
Réalisez ce calcul sur MC-Ed en 8 étapes... |
| [1] | JCGM, « évaluation des données de mesure - Guide pour l'expression de l'incertitude de mesure », BIPM, JCGM 100:2008 (version française), septembre 2008, www.bipm.org. |
| [2] | JCGM, "Evaluation of measurement data - Supplement 1 to the "Guide to the expression of uncertainty in measurement" - Propagation of distributions using a Monte-Carlo method", BIPM, JCGM 101:2008, 2008, www.bipm.org. |
| [3] | AFNOR, « Application de la statistique - Exactitude (justesse et fidelité) des résultats et méthodes de mesure », NF ISO 5725-1 à 6, 1994. |
| [4] | PLATEL F., « Génération de nombres aléatoires pour la méthode de Monte-Carlo », MetGen, Dossier métrologie 21. |
| [5] | PLATEL F., « Quelques générateurs de nombres aléatoires pour la méthode de Monte-Carlo correspondant à des lois utilisées en métrologie », MetGen, Dossier métrologie 23. |
| [6] | PLATEL F., « Outils complémentaires pour la méthode de Monte-Carlo. Le "Pack Monte-Carlo". », MetGen, Dossier métrologie 24. |
| [7] | AFNOR, « Exigences générales concernant la compétence des laboratoires d'étalonnages et d'essais », NF EN ISO/CEI 17025, 2005. |
| [8] | PLATEL F., « Calcul symbolique sur ordinateur - Projet PFS-Algebraic Calculator », MetGen, Dossier divers 2. |
| [9] | PLATEL F., « Calcul de la masse volumique de l'eau », MetGen, Dossier métrologie 18. |
| [10] | BATISTA E., PINTO L., FILIPE E. et VAN DER VEEN A.M.H., "Calibration of micropipettes: Test methods and uncertainty analysis", Measurement, 40, 338-342, 2007. |
| [11] | PLATEL F., « Calcul d'incertitudes avec Gumy », MetGen, Dossier métrologie 4. |