
 |
La question du facteur d'élargissement de Student n'est pas très claire dans la littérature métrologique française. Ce facteur apparaît notamment au travers d'une évaluation d'incertitude en électricité publié par une ancienne association française préposée à la métrologie industrielle et au travers de plaquettes commerciales d'un logiciel payant d'évaluation d'incertitudes. Ces documents sont toutefois très ambigus et de ce fait sources d'erreurs. On peut néanmoins trouver quelques documents plus explicites comme la norme NF EN 60060-2/A11 sur les essais à haute tension ou l'annexe G du GUM, mais ceux-ci ne fournissent aucune démonstration. Dans les lignes qui suivent le lecteur trouvera quelques éléments pour insérer une incertitude évaluée selon une approche de Student dans une évaluation d'incertitudes.
1. Construction de la variable employée
Lorsque l'on veut estimer un intervalle de confiance, et donc une incertitude, sur l'estimation d'une moyenne \( m \) d'une série de mesures \( X_{\text{i}} \) on utilise souvent la variable aléatoire suivante :
| \( \begin{eqnarray}Z = \frac{\bar{X} - m}{ \sigma / \sqrt{n} } \end{eqnarray} \) | (1) |
dans laquelle \( \bar{X} \) est l'estimateur de la moyenne et \( \sigma \) l'écart type.
Il est courant de supposer que la variable aléatoire \( Z \) suit une loi normale. Ceci est évidemment vrai si l'univers des mesures suit une loi normale, et approximativement vrai pour des échantillons de grande taille si l'univers des mesures ne suit pas une loi normale. L'inconvénient de cette expression est que la valeur de l'écart type \( \sigma \) n'est habituellement pas connue. Il semble donc normal de remplacer cette valeur par l'écart type expérimental \( S_{n-1} \) et ainsi d'employer, au lieu de \( Z \), la variable aléatoire :
| \( \begin{eqnarray}T = \frac{\bar{X} - m}{ S_{\text{n}-1} / \sqrt{n} } \end{eqnarray} \) | (2) |
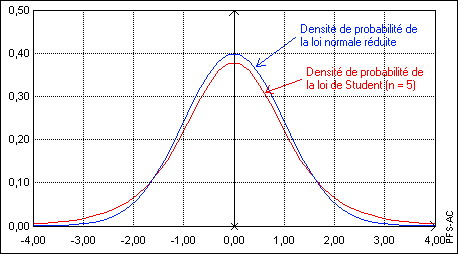
Ceci étant, il reste à déterminer la distribution de \( T \). Bien qu'en moyenne \( S_{\text{n} - 2}^{2} \) est égal à \( \sigma^{2} \), \( S_{\text{n} - 2}^{2} \) est en réalité inférieur à \( \sigma^{2} \) plus de la moitié du temps [1]. Ceci peut nous amener à penser que la distribution de \( T \) est légèrement plus étendue qu'une distribution normale (figure 1). D'autre part, si \( n \) est très grand, \( S_{\text{n} - 2}^{2} \) sera très proche de \( \sigma^{2} \) et nous pouvons croire que pour \( n \) grand la distribution de \( T \) différera peu de la distribution de \( Z \) (c.-à-d., une distribution gaussienne).
On démontre que la variable aléatoire \( T \) suit une loi de Student à \( (n - 1) \) degrés de liberté.
2. Détermination d'un intervalle de confiance pour la moyenne m
Soit \( p \in ]0 ; 1[ \). On cherche \( t_{\text{p}} \), le fractile bilatéral d'ordre \( p \) de la variable aléatoire \( T \) solution de l'équation :
| \( \begin{eqnarray}P~(|T| \leqslant t_{\text{p}}) = p \end{eqnarray} \) . | (3) |
Les équations (2) et (3) conduisent à :
| \( \begin{eqnarray}P~\left(|\bar{X} - m| \leqslant t_{\text{p}} \cdot \left| \frac{S_{\text{n}-1}}{\sqrt{n}} \right|\right) = p \end{eqnarray} \) , | (4) |
autrement dit :
| \( \begin{eqnarray}P~\left(-t_{\text{p}} \cdot \frac{S_{\text{n}-1}}{\sqrt{n}} \leqslant \bar{X} - m \leqslant t_{\text{p}} \cdot \frac{S_{\text{n}-1}}{\sqrt{n}} \right) = p \end{eqnarray} \) . | (5) |
Calcul du fractile tp :
Puisque la variable aléatoire \( T \) suit la loi de Student à \( (n - 1) \) degrés de liberté, le problème se résume à trouver la valeur de \( t_{\text{p}} \) représentée sur la figure 2.
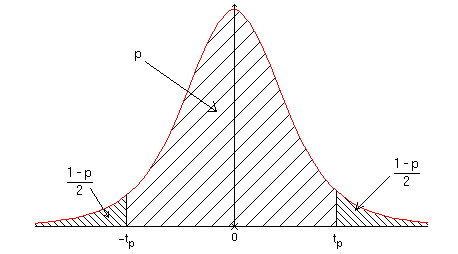
Si on appelle \( \text{FSTU} \) la fonction donnant le fractile de la loi de Student, alors :
| \( \begin{eqnarray}t_{\text{p}} = - \text{FSTU}~\left( n - 1~;~\frac{1 - p}{2} \right) \end{eqnarray} \) . | (6) |
Pratiquement, la valeur de \( t_{\text{p}} \) peut être obtenue en utilisant la table des fractiles de la loi de Student extraite de la référence [2] (page 43) reproduite dans le lien ci-dessous :
 |
fractiles tp de la loi de Student. |
Remarque : dans ce tableau, \( t_{\text{p}} \) s'obtient pour la probabilité \( (1 - p) / 2 \).
Cette valeur peut également être calculée directement avec le logiciel PFS-AC (cf. figure 3) téléchargeable dans le dossier divers de ce site, à l'aide de l'équation suivante (décompresser le fichier dans le répertoire de l'application PFS-AC) :
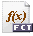 |
équation PFS-AC donnant tp (saisir N et p dans la zone de définition des variables). |
Remarque : dans ce fichier \( N \) est le nombre de degrés de liberté.
La mesure d'une tension avec un multimètre a donné les valeurs suivantes :
| Mesure n° \( i \) |
Valeur (en mV) \( x_{\text{i}} \) |
| \( 1 \) | \( 100,125 \) |
| \( 2 \) | \( 100,117 \) |
| \( 3 \) | \( 100,109 \) |
| \( 4 \) | \( 100,119 \) |
La valeur moyenne de la tension est : \( 100,118~\text{mV} \).
L'écart type expérimental vaut : \( 0,006~61~\text{mV} \).
Pour un niveau de confiance de 95,45 % \( (p = 0,9545) \) et 3 degrés de libertés, on trouve à l'aide de PFS-AC un fractile valant : \( 3,31 \).
Ainsi la moyenne vaut : \( 100,118~\text{mV} \) avec une incertitude (à 95,45 %) de \( 0,011~\text{mV} \).
4. Insertion dans une évaluation d'incertitudes
En posant \( k_{\text{p}} \) le coefficient d'élargissement pour un niveau de confiance de \( p \) pour cents, d'après la loi de propagation des variances [3], l'incertitude élargie s'écrit :
| \( \begin{eqnarray}U(y) = k_{\text{p}} \cdot \sqrt{ \sum_{\text{i} = 1}^\text{n} c_\text{i}^2\;\cdot\;u^2(x_\text{i}) + 2\;\cdot\;\sum_{\text{i} = 1}^{\text{n} - 1} \sum_{\text{j} = \text{i} + 1}^\text{n} c_\text{i}\:\cdot\;c_\text{j}\;\cdot\;u(x_\text{i})\,\cdot\;u(x_\text{j})\;\cdot\;r(x_\text{i}, x_\text{j})}\end{eqnarray} \) , | (7) |
soit :
| \( \begin{eqnarray}U(y) = \sqrt{ \sum_{\text{i} = 1}^\text{n} c_\text{i}^2\;\cdot \left(k_{\text{p}} \cdot u(x_\text{i})\right)^{2} + 2\;\cdot\;\sum_{\text{i} = 1}^{\text{n} - 1} \sum_{\text{j} = \text{i} + 1}^\text{n} c_\text{i}\:\cdot\;c_\text{j}\;\cdot\;(k_{\text{p}} \cdot u(x_\text{i}))\,\cdot\;(k_{\text{p}} \cdot u(x_\text{j}))\;\cdot\;r(x_\text{i}, x_\text{j})}\end{eqnarray} \) . | (8) |
Dans les calculs \( (k_{\text{p}} \cdot u(x_\text{i})) \) représente l'incertitude élargie. Afin de conserver le formalisme du GUM [3], dans l'évaluation d'incertitudes, on remplacera donc \( (S_{\text{n}-1} / \sqrt{n}) \) par \( (t_{\text{p}} / k_{\text{p}}) \cdot (S_{\text{n}-1} / \sqrt{n}) \). Ce qui revient à prendre l'incertitude type de répétabilité :
| \( \begin{eqnarray}u_{\text{r}} = \frac{t_{\text{p}}}{k_{\text{p}}} \cdot \frac{S_{\text{n}-1}}{\sqrt{n}} \end{eqnarray} \) . | (9) |
Ainsi lorsqu'elle sera élargie par multiplication de \( k_{\text{p}} \) dans la formulation du GUM [3], on retrouvera bien l'élargissement de Student :
| \( \begin{eqnarray}U_{\text{r}} = t_{\text{p}} \cdot \frac{S_{\text{n}-1}}{\sqrt{n}} \end{eqnarray} \) . | (10) |
Remarque : l'élargissement au moyen du facteur de Student conduit à multiplier l'écart type expérimental par un facteur : il ne faut cependant pas en déduire que ce facteur vise à corriger l'estimation de l'écart type. En effet, ce facteur est construit pour donner un intervalle de confiance de la moyenne et non une meilleure estimation de l'écart type. Si on s'intéresse à l'écart type, il faut alors déterminer un intervalle de confiance de l'écart type en utilisant une méthode similaire avec la loi du khi-2. Ce type de calcul trouve des applications dans le domaine des cartes de contrôles ou on peut être amené à suivre l'évolution de l'écart type d'une grandeur. Dans le domaine des évaluations d'incertitudes celui-ci n'est pas appliqué : cela reviendrait à évaluer l'incertitude d'une incertitude...
5. Calcul avec Gumy (à partir de la version 1.40)
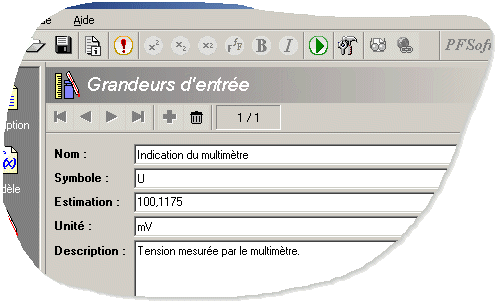
Reprenons l'exemple numérique donné précédemment. Commençons par définir la grandeur mesurée comme représenté sur la figure 4.
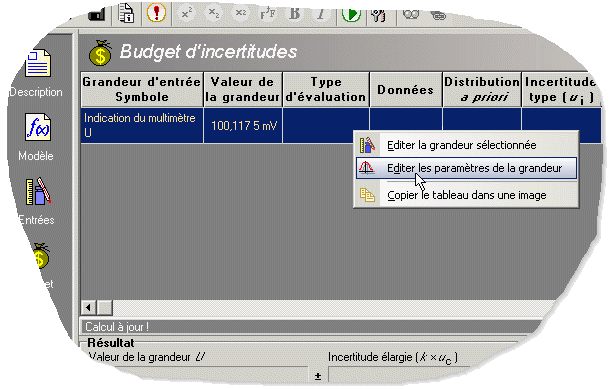
Dans le volet de visualisation du budget d'incertitudes sélectionnez la ligne de la grandeur considérée par un clique gauche puis activez le menu pop up correspondant par un clique droit et sélectionnez l'option d'édition des paramètres de la grandeur comme indiqué sur la figure 5.
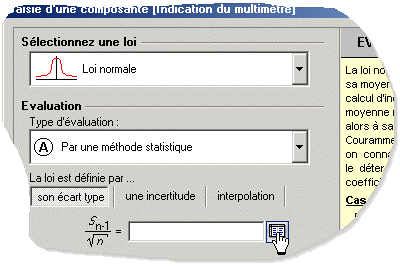
Compte tenu de la remarque précédente définissez la loi comme étant normale, puis sélectionnez l'option de calcul par une méthode de type A. Enfin activez l'écran de calcul de l'incertitude type comme indiqué sur la figure 6.
Saisissez les mesures comme indiqué sur la figure 7 puis calculez l'incertitude.
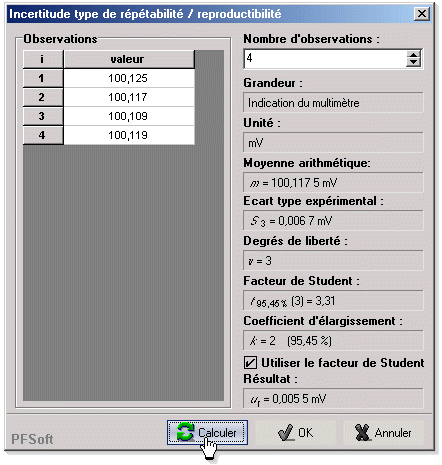
Le calcul est maintenant terminé. Lorsque vous exécuterez l'option permettant de réaliser un rapport d'incertitude, vous obtiendrez un texte ayant la forme représenté sur la figure 8.
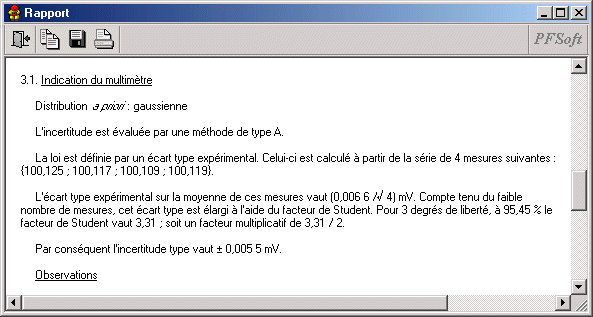
Remarque : à l'incertitude type de \( 0,005~5~\text{mV} \) de la figure 8 correspond une incertitude élargie de \( 0,011~\text{mV} \), ce qui correspond au calcul fait « à la main » précédemment.
6. Quand utiliser le facteur de Student ?
La question qui se pose couramment est : en dessous de combien de mesures doit-on utiliser le facteur de Student ? On peut trouver dans la littérature métrologique des tentatives de réponse à cette question. Par exemple, la référence [4] recommande d'utiliser l'élargissement au moyen d'un test de Student en dessous de six degrés de libertés, soit sept mesures pour un niveau de confiance de 95,45 %. Compte tenu de ce qui précède, cette réponse n'a pas vraiment de sens, et on peut même dire qu'elle est fausse, qu'elle engendre une sous-estimation non négligeable de l'incertitude.
Cette réponse n'a pas de sens puisque comme on a vu précédemment, à partir du moment où on utilise un écart type expérimental, la variable aléatoire (notée \( T \) au paragraphe 1) qui permet d'évaluer l'incertitude sur la moyenne suit forcément une loi de Student. Donc en toute rigueur, on devrait systématiquement utiliser l'élargissement de Student avec un écart type expérimental. D'autre part, c'est dangereux de considérer que l'on ne doit plus utiliser le facteur de Student au dessus de sept observations. En effet, la figure 9 représente le graphe de \( (t_{\text{p}}/k_{\text{p}} - 1) \cdot 100 \) en fonction du nombre de mesures (\( t_{\text{p}} \) et \( k_{\text{p}} \) correspondent aux les notations du paragraphe 4) pour un niveau de confiance de 95,45 %. Autrement dit, le graphe représente la sous-évaluation commise en utilisant un écart type expérimental et sans utiliser un élargissement de Student en fonction du nombre de mesures.
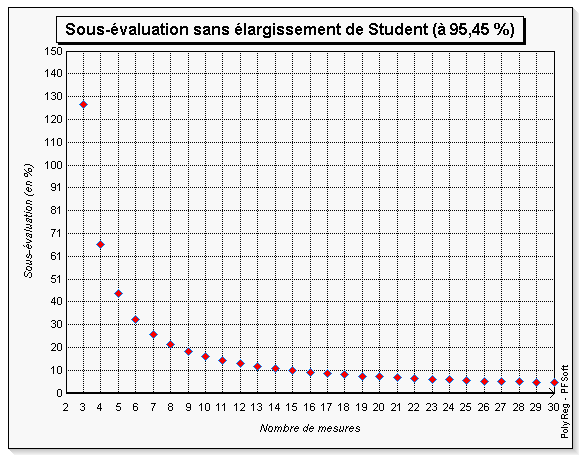
Pour sept mesures, l'incertitude de répétabilité est sous-évaluée de 26 %, ce qui paraît excessif. En revanche, l'erreur devient inférieure à 10 % à partir 15 mesures, ce qui est déjà « plus acceptable ».
Toutefois, la sous-évaluation est également liée au niveau de confiance recherché. La figure 10 représente la sous-évaluation de l'incertitude pour un niveau de confiance de 99,73 %. On constate que la sous-évaluation passe sous la barre des 10 % à partir de 29 mesures.
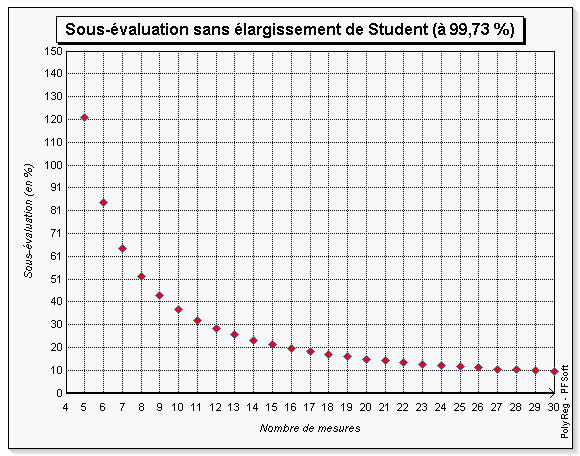
En conclusion, dans un certain nombre de cours de statistiques, l'on conseille d'utiliser l'écart type expérimental en dessous de 30 observations (la formule de l'écart type présentant un biais relatif en \( \left(^{1}\!/\!_{2 \cdot n}\right) \) [5]). Il semble tout à fait raisonnable d'utiliser l'élargissement de Student jusqu'à 30 mesures sur cet écart type expérimental. L'utilisation d'un outil tel que Gumy permet d'automatiser ce calcul.
| [1] | DIXON W.J., MASSEY F.J., "Introduction to statistical analysis", McGraw-Hill Book Compagny, New York, 1951. |
| [2] | « Tables statistiques », Revue de Statistique Appliquée, 1973. |
| [3] | JCGM, « Evaluation des données de mesure - Guide pour l'expression de l'incertitude de mesure », BIPM, JCGM 100:2008 (version française), septembre 2008, www.bipm.org. |
| [4] | « Guide Eurachem / CITAC - Quantifier l'Incertitude dans les Mesures Analytiques », Eurachem, Deuxième édition, Version française, 2000. |
| [5] | FEMENIAS J.-L., « Probabilités et statistique pour les sciences physiques », Dunod, 2003. |