
 |
Cette loi est utilisée en métrologie en particulier pour calculer l'incertitude sur des grandeurs oscillant autour d'une valeur. C'est par exemple typiquement le cas de la température dans un bain thermostaté qui va osciller autour de sa température de consigne. Cette loi est peu documentée dans la littérature mathématique ou l'on trouve toutefois la loi dite de « l'Arc sinus » qui est très voisine. Afin de pallier ce manque de documentation, le lecteur trouvera dans ce dossier les justifications mathématiques qui permettent de valider dans le cadre d'un système qualité l'utilisation de la loi dérivée d'Arc sinus dans les calculs d'incertitude.
Soit \( X \) une variable aléatoire à valeurs dans \( ]-1~;~1[ \). La variable aléatoire \( X \) est dite suivre la loi de l'Arc sinus si elle est absolument continue et si elle admet pour densité de probabilité la fonction :
| \( \begin{eqnarray}f_{\text{X}} = \frac{1}{\pi} \cdot \frac{1}{ \sqrt{1 - x^{2}}}\quad\end{eqnarray} \) pour \(\quad -1 < x < 1 \) . | (1) |
Remarques :
- cette loi est en fait un cas particulier de la
loi Bêta
B (½, ½) ;
- on parle de loi de l'Arc sinus car la fonction de répartition de cette loi fait
intervenir une fonction Arc sinus.
2.1. Expression de la densité de probabilité
Soit \( X \) une grandeur oscillant avec une amplitude \( a \) et une période \( T \) autour d'une valeur \( b \). L'équation donnant la valeur \( x \) en fonction du temps \( t \) est de la forme :
| \( \begin{eqnarray}x(t) = a \cdot \sin (\omega) \end{eqnarray} \) , | (2) |
avec \( \omega \) la pulsation définie par :
| \( \begin{eqnarray}\omega = \frac{2 \times \pi}{T} \end{eqnarray} \) . | (3) |
Afin de simplifier, compte tenu des propriétés de symétrie et de périodicité de la fonction sinus on restreint l'étude à l'intervalle \( [-\pi / 2~;~\pi / 2 ] \) sur lequel cette fonction est monotone. Sur la demi-période considérée, la probabilité pour \( x \) d'être entre \( x \) et \( x + \Delta x \) est égale au rapport du temps \( \Delta t \) pendant lequel on est entre \( x \) et \( x + \Delta x \) divisé par la demi-période \( ^{T}\!/_{2} \). En notant \( \Delta p(x) \) cette probabilité on a :
| \( \begin{eqnarray} \Delta p(x) = \frac{ \Delta t }{ ^{T}\!/_{2} } \end{eqnarray} \) . | (4) |
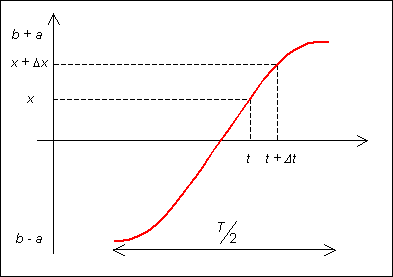
Dans ces conditions,
| \( \left\{ \begin{array}{l} t = \dfrac{1}{\omega} \cdot \arcsin \left( \dfrac{ x - b }{ a } \right) \\[1ex] t + \Delta t = \dfrac{1}{\omega} \cdot \arcsin \left( \dfrac{ x - b + \Delta x }{ a } \right) \end{array} \right. \) . | (5) |
A partir de (3) et (4) on obtient :
| \( \begin{eqnarray} \frac{\Delta p(x)}{ \Delta x } = \frac{1}{ \pi \cdot a } \cdot \frac{ \arcsin \left( \dfrac{ x - b + \Delta x }{ a } \right) - \arcsin \left( \dfrac{ x - b }{ a } \right) }{ \dfrac{ \Delta x }{ a } } \end{eqnarray} \) . | (6) |
En faisant tendre \( \Delta x \) vers 0 on obtient (dérivée de l'Arc sinus) :
| \( \begin{eqnarray} \frac{ dp }{ dx }(x) = \frac{ 1 }{ \pi \cdot a } \cdot \frac{ 1 }{ \sqrt{ 1 - \left( \dfrac{ x - b }{ a } \right)^{2} }} \end{eqnarray} \) . | (7) |
Par définition, la densité de probabilité est égale à :
| \( \begin{eqnarray} \rho (x) = \frac{ dp }{ dx }(x) \end{eqnarray} \) . | (8) |
D'où
| \( \begin{eqnarray} \rho (x) = \frac{ 1 }{ \pi \cdot a } \cdot \frac{ 1 }{ \sqrt{ 1 - \left( \dfrac{ x - b }{ a } \right)^{2} }} \quad \text{avec} \quad b - a < x < b + a \quad \text{.} \end{eqnarray} \) | (9) |
Remarque : pour \( b = 0 \) et \( a = 1 \) on retrouve la loi de l'Arc sinus.
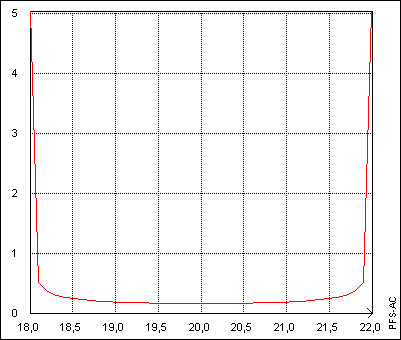
Un exemple de densité de probabilité est représenté sur la figure 2. La forme de la courbe explique que l'on parle souvent de distribution en « U ».
Par définition, la moyenne vaut :
| \( \begin{eqnarray} m = \int_{b - a}^{b + a} x \cdot \rho (x) \cdot dx \end{eqnarray} \) . | (10) |
En appliquant la formule (9) à cette expression, on obtient :
| \( \begin{eqnarray} m = \int_{b - a}^{b + a} \frac{ 1 }{ \pi \cdot a } \cdot \frac{ 1 }{ \sqrt{ 1 - \left( \dfrac{ x - b }{ a } \right)^{2} }} \cdot dx \quad \text{.} \end{eqnarray} \) | (11) |
Cette intégrale se calcule en effectuant le changement de variable suivant :
| \( \begin{eqnarray} x = a \cdot \sin (u) + b \end{eqnarray} \) , | (12) |
qui conduit à :
| \( \begin{eqnarray} m = \int_{-\pi / 2}^{\pi / 2} \frac{ 1 }{ \pi } \cdot \Bigl( a \cdot \sin (u) + b \Bigr) \cdot du \end{eqnarray} \) , | (13) |
et donc :
| \( \begin{eqnarray} m = b \end{eqnarray} \) . | (14) |
Par définition, la variance vaut :
| \( \begin{eqnarray} v = \int_{b - a}^{b + a} x^{2} \cdot \rho (x) \cdot dx - m^{2} \end{eqnarray} \) . | (15) |
Compte tenu de (14) et de (9) on obtient :
| \( \begin{eqnarray} v = \int_{b - a}^{b + a} \frac{ 1 }{ \pi \cdot a } \cdot \frac{ x^{2} }{ \sqrt{ 1 - \left( \dfrac{ x - b }{ a } \right)^{2} }} \cdot dx - b^{2} \quad \text{.} \end{eqnarray} \) | (16) |
En utilisant le changement de variable (12), cette expression devient :
| \( \begin{eqnarray} v = \int_{-\pi / 2}^{\pi / 2} \frac{ 1 }{ \pi } \cdot \frac{ \bigl(a \cdot \sin u + b\bigr)^{2} }{ \sqrt{ 1 - \sin^{2} (u)} } \cdot \cos (u) \cdot du - b^{2} \quad \text{.} \end{eqnarray} \) | (17) |
En utilisant les formules de trigonométrie on obtient successivement :
| \( \begin{eqnarray} v = \int_{-\pi / 2}^{\pi / 2} \frac{ 1 }{ \pi } \cdot \frac{ a^{2} \cdot \sin^{2}(u) + 2 \times a \cdot b \cdot \sin(u) + b^{2} }{ \cos(u) } \cdot \cos (u) \cdot du - b^{2} \quad \text{,} \end{eqnarray} \) |
| \( \begin{eqnarray} v = \int_{-\pi / 2}^{\pi / 2} \frac{ 1 }{ \pi } \cdot \bigl( a^{2} \cdot \sin^{2}(u) + 2 \times a \cdot b \cdot \sin(u) + b^{2} \bigr) \cdot du - b^{2} \quad \text{,} \end{eqnarray} \) |
| \( \begin{eqnarray} v = \int_{-\pi / 2}^{\pi / 2} \frac{ a^{2} }{ \pi } \cdot \frac{ 1 - \cos (2 \times u) }{ 2 } \cdot du + \int_{-\pi / 2}^{\pi / 2} \frac{ 2 \times a \cdot b }{ \pi } \cdot \sin(u) \cdot du + \int_{-\pi / 2}^{\pi / 2} \frac{ 1 }{ \pi } \cdot b^{2} \cdot du - b^{2} \quad \text{.} \end{eqnarray} \) |
Ce qui donne :
| \( \begin{eqnarray} v = \frac{ a^{2} }{ \pi } \cdot \Biggl[ \frac{ u }{ 2 } - \frac{ 1 }{ 4 } \cdot \sin (2 \times u) \Biggr]_{-\pi / 2}^{ \pi / 2 } + \frac{ 2 \times a \cdot b }{ \pi } \cdot \Biggl[ - \cos (u) \Biggr]_{-\pi / 2}^{ \pi / 2 } + \frac{ b^{2} }{ \pi } \cdot \Biggl[~u~\Biggr]_{-\pi / 2}^{ \pi / 2 } - b^{2} \quad \text{.} \end{eqnarray} \) |
D'où
| \( \begin{eqnarray} v = \frac{ a^{2} }{ 2 } \end{eqnarray} \) . | (18) |
Remarque : dans certains cas on assimile la régulation à une loi uniforme en argumentant que la loi uniforme est très pénalisante. En réalité on sous-évalue l'incertitude puisque la variance dans le cas d'une loi uniforme vaut \( a^{2} / 3 \).
2.4. Expression de la fonction de répartition
Par définition, en conservant les notations précédentes, la fonction de répartition est :
| \( \begin{eqnarray} F(x) = \int_{b - a}^{x} \rho (x) \cdot dx \end{eqnarray} \) , | (19) |
c'est à dire avec (9) :
| \( \begin{eqnarray} F(x) = \int_{b - a}^{x} \frac{ 1 }{ \pi \cdot a } \cdot \frac{ 1 }{ \sqrt{ 1 - \left( \dfrac{ x - b }{ a } \right)^{2} }} \cdot dx \quad \text{,} \end{eqnarray} \) | (20) |
ce qui donne :
| \( \begin{eqnarray} F(x) = \frac{1}{\pi} \cdot \Biggl[ \arcsin \left( \frac{ x - b }{ a } \right) + \frac{\pi}{2} \Biggr]\quad \text{avec} \quad b - a \leqslant x \leqslant b + a \quad \text{.} \end{eqnarray} \) | (21) |
On a représenté sur la figure 3 l'allure de la fonction de répartition.
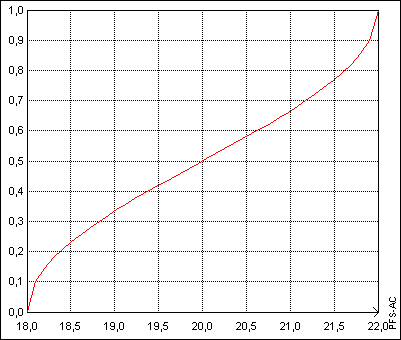
2.5. Réciproque de la fonction de répartition
La réciproque est utilisée pour la génération de nombres aléatoires dans le cadre des simulations de Monte-Carlo [1].
En conservant les notations précédentes, soit \( F(x) \in [-1~;~1] \). A partir de la formule (21) on obtient :
| \( \begin{eqnarray} x = -a \cdot \cos \bigl[\pi \cdot F(x)\bigr] + b \end{eqnarray} \) . | (22) |
| [1] | PLATEL F., « Quelques générateurs de nombres aléatoires pour la méthode de Monte-Carlo correspondant à des lois utilisées en métrologie », |