
 |
On a vu dans [1]. comment générer des échantillons d'une variable aléatoire suivant une loi uniforme. Si cette loi occupe une place importante dans le cadre des calculs d'incertitude en métrologie on rencontre également d'autres lois. Les principales sont : la loi normale, la loi dérivée d'Arc sinus et dans une moindre mesure la loi triangulaire ou la loi trapézoïdale.
1. Méthode de la transformation réciproque
Il s'agit là d'une méthode générale permettant de générer des échantillons suivant une loi donnée pour peu que l'on dispose de la réciproque de sa fonction de répartition. Soient FX la fonction de répartition de la variable aléatoire X suivant la loi que l'on veut simuler, et U la loi uniforme U(0,1). On cherche à déterminer la loi suivie par la variable aléatoire \( F_{\text{X}}^{-1}(U) \). Pour cela on cherche sa fonction de répartition définie par \( P(F_{\text{X}}^{-1}(U) \leqslant x) \) pour tout réel x. Comme FX est croissante (propriété des fonctions de répartition) :
| \( P(F_{\text{X}}^{-1}(U) \leqslant x) = P(U \leqslant F_{\text{X}}(x)) \) . | (1) |
Dans le membre de droite de l'équation (1) on reconnaît la fonction de répartition de U évaluée au point FX (x). Sachant que la fonction de répartition de la loi uniforme est la fonction identité (pour tout \( y \in [0~;~1] \) on a \( P(U \leqslant y) = y \)) on déduit de (1) :
| \( P(F_{\text{X}}^{-1}(U) \leqslant x) = F_{\text{X}}(x) \) . | (2) |
Donc la fonction de répartition de la variable aléatoire \( F_{\text{X}}^{-1}(U) \) est \( F_{\text{X}} \). Pour une loi donnée, la fonction de répartition étant unique, on déduit que \( F_{\text{X}}^{-1}(U) \) suit la même loi que X. En conclusion pour générer un échantillons de n valeurs d'une variable aléatoire X ayant une fonction de répartition FX, il suffit de générer un échantillons de n valeurs u1, ...,un d'une variable aléatoire uniforme suivant U(0,1). Puis de calculer \( F_{\text{X}}^{-1}(u_{1}) \), ..., \( F_{\text{X}}^{-1}(u_{\text{n}}) \) qui est un échantillon suivant la loi de X.
Remarque 1 : dans la littérature on trouve parfois cette méthode appelée « méthode de la transformation inverse » ou « méthode de l'inversion ». Il semble qu'il s'agisse d'une erreur de traduction de l'expression anglaise "inversion method". Le terme anglais "inversion" est en effet un faux ami qui en français se traduit « réciproque » pour une fonction. En français, le terme « inverse » a bien évidemment un autre sens.
Remarque 2 : ce type de méthode d'usage courant en mathématiques est une anamorphose (transformation qui a un objet fait correspondre l'objet dont il est l'image).
2. Application à la loi dérivée d'Arc sinus
Soit X une variable aléatoire suivant la loi dérivée d'Arc sinus de moyenne b et de demi-étendue a. D'après [2], la réciproque de la fonction de répartition de X est :
| \( F^{-1} (y) = -a \cdot \cos (\pi \cdot y) + b \) pour \( y \in [0~;~1] \) . | (3) |
On génère une ensemble \( \{ u_{\text{i}} \}_{1 \leqslant \text{i} \leqslant \text{n}} \) de valeurs d'une variable aléatoire uniforme U(0,1). Par application de la méthode de la transformation réciproque, l'ensemble \( \{ -a \cdot \cos (\pi \cdot u_{\text{i}}) + b \}_{1 \leqslant \text{i} \leqslant \text{n}} \) correspond à un échantillon distribué selon la loi dérivée d'Arc sinus de moyenne b et de demi-étendue a.
Cet algorithme a été mis en oeuvre dans le programme darcsin.exe téléchargeable dans le lien ci-dessous :
 |
La figure 1 représente un exemple d'échantillon généré par ce programme
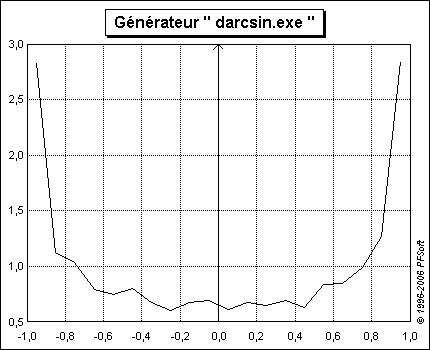
Le programme darcsin.exe fonctionne en mode ligne de commande DOS. Il nécessite un échantillon de valeurs distribué uniformément qui peut être produit par un générateur de la référence [1]. Le principe de fonctionnement est reproduit sur la figure 2.
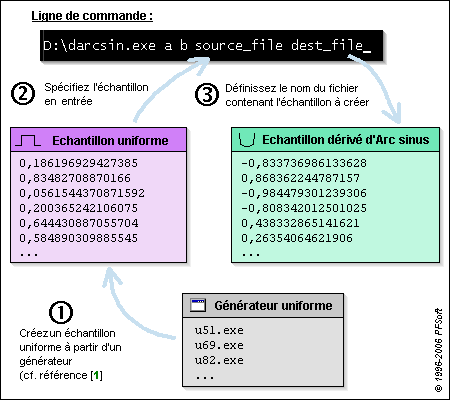
3. Application à la loi triangulaire
Cette loi est utilisée dans les cas où on estime qu'une valeur proche des bornes d'un intervalle est peu probable (figure 3). Par exemple si on a estimé que la dérive d'une cale étalon pouvait être au maximum de 30 nm (à partir d'une étude sur plusieurs cales), mais que le suivi dans le temps d'une cale particulière indique qu'elle ne dérive pas, alors on prendra une loi triangulaire pour calculer la composante d'incertitude liée à la dérive de cette cale (moyenne = 0 ; demi-étendue = 30 nm ; écart type = 7,1 nm).
Soit X une variable aléatoire suivant la loi triangulaire de moyenne b et de demi-étendue a. La fonction de répartition de X est :
| \( F(x) = \begin{cases} 0 \quad \text{si} \quad x \in ]-\infty~;~b - a[~\text{,} \\[1ex] \dfrac{(x - b + a)^{2}}{2 \cdot a^{2}} \quad \text{si} \quad x \in [b - a~;~b]~\text{,} \\[1ex] \dfrac{-x^{2} + 2 \cdot (a+ b) \cdot (x - b) + b^{2}}{2 \cdot a^{2}} + \dfrac{1}{2} \quad \text{si} \quad x \in ]b~;~b + a]~\text{,} \\[1ex] 1 \quad \text{si} \quad x \in ]b + a~;~+\infty[~\text{.} \end{cases} \) | (4) |
La réciproque de cette fonction est :
| \( F^{-1}(y) \begin{cases} a \cdot \sqrt{2 \cdot y} + b - a & \text{si} \quad y \in [0~;~0,5]~\text{,} \\[1ex] a \cdot \left[1 - \sqrt{2 \cdot (1 - y)} \right] + b & \text{si} \quad y \in ]0,5~;~1[~\text{.} \end{cases} \) | (5) |
On génère un ensemble \( \{ u_{\text{i}} \}_{1 \leqslant \text{i} \leqslant \text{n}} \) de valeurs d'une variable aléatoire uniforme U(0,1). Par application de la méthode de la transformation réciproque, l'ensemble \( \{F^{-1}(u_{\text{i}})\}_{1 \leqslant \text{i} \leqslant \text{n}} \) correspond à une distribution de la loi triangulaire de moyenne b et de demi-étendue a.
Cet algorithme a été mis en oeuvre dans le programme triang.exe téléchargeable dans le lien ci-dessous :
 |
La figure 4 représente un exemple d'échantillon généré par ce programme.
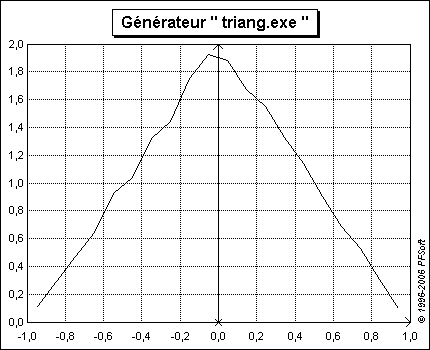
Le principe de fonctionnement est identique à darcsin (se reporter à la figure 2).
4. Application à la loi trapézoïdale
Soit X une variable aléatoire à valeurs réelles. On dit que X suit une loi trapézoïdale si la fonction densité de probabilité a une forme de trapèze comme indiqué sur la figure 6. Cette distribution peut être définie par quatre paramètres a, b, c et d (représentés sur la figure 5) avec :
| a : la limite inférieure de la distribution ; | |
| b : la limite supérieure ; | |
| c : le premier sommet ; | |
| d : le second sommet. |
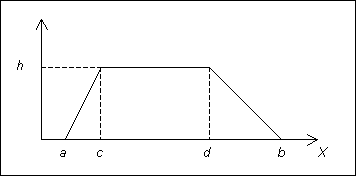
Dans les lignes qui suivent on notera cette loi T(a, c, d, b). Afin de satisfaire la condition de normalisation de la densité de probabilité, la valeur de h vaut :
| \( \begin{eqnarray} h = \dfrac{2}{b - a + d - c} \end{eqnarray} \) . | (6) |
La réciproque F-1 de la fonction de répartition s'obtient aisément et vaut (cf. [3]) :
| \( F^{-1}(y) \begin{cases} a + \sqrt{\dfrac{2 \cdot (c - a)}{h}} \cdot \sqrt{h} & \text{si} \quad y \in [c_{0}~;~c_{1}]~\text{,} \\[1ex] \dfrac{a + c}{2} + \dfrac{y}{h} & \text{si} \quad y \in [c_{1}~;~c_{2}]~\text{,} \\[1ex] b - \sqrt{\dfrac{2 \cdot (b - d)}{h}} \cdot \sqrt{1 - y} & \text{si} \quad y \in [c_{2}~;~c_{3}]~\text{.} \end{cases} \) | (7) |
avec :
| \( \left\{ \begin{array}{l} c_{0} = 0 \\[1ex] c_{1} = \dfrac{h}{2} \cdot (c - a) \\[1ex] c_{2} = 1 - \dfrac{h}{2} \cdot (b - d) \\[1ex] c_{3} = 1 \end{array} \right. \) . | (8) |
On génère un ensemble \( \{ u_{\text{i}} \}_{1 \leqslant \text{i} \leqslant \text{n}} \) de valeurs d'une variable aléatoire uniforme U(0,1). Par application de la méthode de la transformation réciproque, l'ensemble \( \{ F^{-1}(u_{\text{i}}) \}_{1 \leqslant \text{i} \leqslant \text{n}} \) correspond à une distribution de la loi trapézoïdale T(a, c, d, b).
Cet algorithme a été mis en oeuvre dans le programme trapez.exe téléchargeable dans le lien ci-dessous :
 |
La figure 6 représente un exemple d'échantillon généré par ce programme.
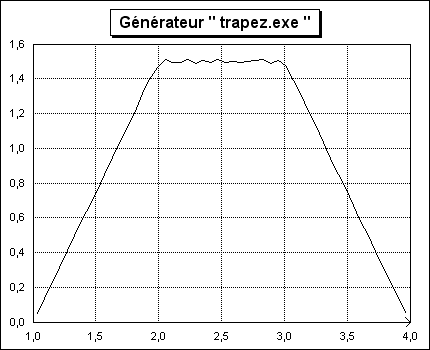
Le principe de fonctionnement est identique à darcsin (se reporter à la figure 2).
Le générateur trapez.exe est en fait extrêmement ouvert et permet de générer plusieurs lois. Le tableau 1 représente l'ensemble des lois qu'il est possible de simuler en fonction des paramètres saisis.
| Paramètres | Distribution | |
| a < c < d < b |  |
trapèze |
| a = c < d < b |  |
rectangle - trapèze |
| a < c = d < b | 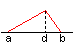 |
triangle |
| a < c < d = b | 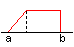 |
trapèze - rectangle |
| a = c = d < b | 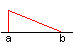 |
triangle |
| a = c < d = b | 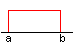 |
rectangle |
| a < c = d = b |  |
triangle |
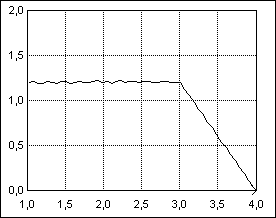
La figure 7 représente des échantillons générés pour différents paramètres avec trapez.exe.
 |
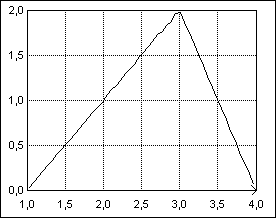 |
| a = 1 ; c = 1 ; d = 3 ; b = 4 | a = 1 ; c = 3 ; d = 3 ; b = 4 |
 |
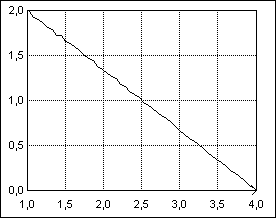 |
| a = 1 ; c = 2 ; d = 4 ; b = 4 | a = 1 ; c = 1 ; d = 1 ; b = 4 |
 |
 |
| a = 1 ; c = 1 ; d = 4 ; b = 4 | a = 1 ; c = 4 ; d = 4 ; b = 4 |
5. Cas de la loi normale
Dans le cas de la loi normale, on utilise la transformation de Box-Muller [4]. Comme précédemment il s'agit de transformer une distribution suivant une loi uniforme en distribution suivant une loi normale.
Soient u1 et u2, deux nombres aléatoires indépendants provenant d'une distribution uniforme. On calcule :
| \( \left\{ \begin{array}{l} z_{1} = \sqrt{-2 \cdot \ln (u_{1})} \cdot \cos (2 \cdot \pi \cdot u_{2}) \\[1ex] z_{2} = \sqrt{-2 \cdot \ln (u_{1})} \cdot \sin (2 \cdot \pi \cdot u_{2}) \end{array} \right. \) . | (9) |
Les variables z1 et z2 suivent une loi normale centrée réduite.
Ensuite pour obtenir un échantillon généré par une variable aléatoire suivant par la loi N (µ, σ2) on calcule :
| xi = µ + σ · zi | (10) |
Cet algorithme a été mis en oeuvre dans le programme norm.exe téléchargeable dans le lien ci-dessous :
 |
La figure 8 représente un exemple d'échantillon généré par ce programme
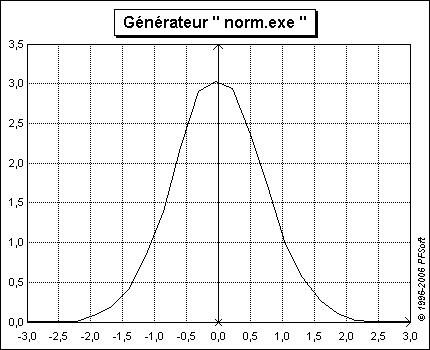
Le principe de fonctionnement est identique à darcsin (se reporter à la figure 2).
Remarque : on peut également sommer des variables aléatoires indépendantes réparties uniformément pour obtenir une variable aléatoire suivant une loi normale. En effet, par application du théorème de la limite centrale et par convolution des densités on montre qu'en sommant déjà trois variables aléatoires la densité est très proche d'une loi normale. On montre qu'à partir de dix variables aléatoires l'assimilation à une loi normale est raisonnable. Ceci étant, cette méthode pour générer des nombres aléatoires sur ordinateur n'est pas véritablement réaliste car elle nécessite un trop grand nombre de valeurs suivant une loi uniforme. Par exemple pour générer un échantillon de loi normale de 10 000 valeurs, il faut générer 100 000 valeurs suivant une loi uniforme...
| [1] | PLATEL F., « Génération de nombres aléatoires pour la méthode de Monte-Carlo », MetGen, Dossier métrologie 21. |
| [2] | PLATEL F., « La loi dérivée d'Arc sinus », MetGen, Dossier métrologie 22. |
| [3] | KACKER R.N. et LAWRENCE J., "Trapezoidal and triangular distributions for Type B evaluation of standard uncertainty", Metrologia, 44, 117-127, 2007. |
| [4] | BOX G.E.P. et MULLER M., "A note on the generation of random normal deviates", Annals of Mathematical Statistics, 29, 610-611, 1958. |