Outils pour la méthode de Monte-Carlo

Nous avons vu dans [1] et [2] comment générer des échantillons distribués selon les lois les plus courantes en métrologie. L'objectif de ce dossier est d'utiliser les générateurs développés pour effectuer des calculs d'incertitudes en propageant les distributions selon la méthode de Monte-Carlo à l'aide d'un ensemble de logiciels constituant le Pack Monte-Carlo.

1. Introduction

Dans ce dossier, nous supposons connu le modèle de la mesure et nous utiliserons les notations suivantes :

\( \begin{array}{l} f : & \mathbb{R}^{\text{p}} & \to & \mathbb{R} \\ & (x_{1},\ldots~, x_{\text{p}}) & \mapsto & y = f(x_{1},\ldots~, x_{\text{p}}) \end{array} \)

D'autre part pour i ∈ [1 ; p] la loi de la grandeur d'entrée X_i est connue et l'on notera x_i une réalisation de cette grandeur. De même y est une réalisation de la grandeur de sortie Y.

La méthode de Monte-Carlo dont le principe est rappelé dans [1] permet d'obtenir directement la distribution de la grandeur de sortie du modèle à partir de simulations des grandeurs d'entrée. L'objet de ce dossier est de décrire comment réaliser ces opérations dans la pratique depuis la préparation de l'échantillon d'entrée jusqu'à la création de l'échantillon de sortie. L'ensemble du processus est représenté sur la figure 1.

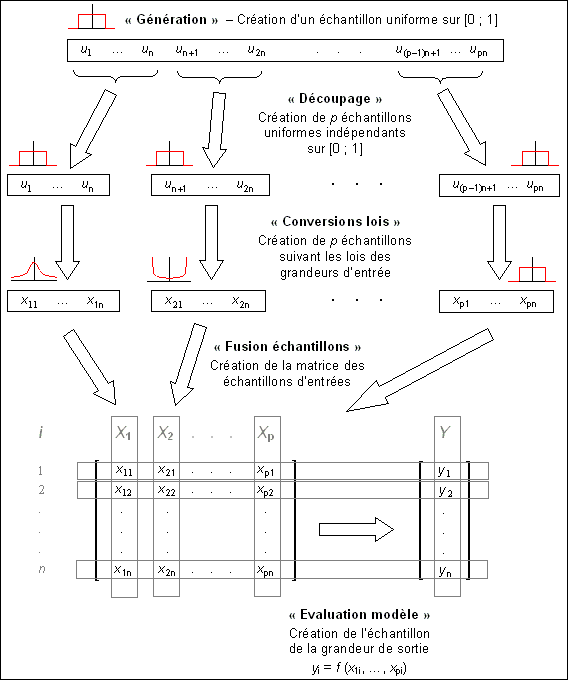
Fig. 1. - Obtention de l'échantillon de sortie

Tout d'abord il est nécessaire de définir la taille n de l'échantillon de sortie. Dans la pratique il est fréquent de prendre n = 10⁶. La première étape consiste à générer un échantillon uniforme de taille n ·; p. Pour ce faire, plusieurs générateurs (u51, u69, u82) ont été définis dans [1]. Ensuite cet échantillon est « découpé » en p échantillons à l'aide du logiciel split (cf. §2). A l'issue de cette opération on dispose de p échantillons indépendants et uniformes de valeurs entre 0 et 1. L'étape suivante consiste à transformer ces échantillons pour qu'ils correspondent aux lois suivies par les grandeurs d'entrée. Les programmes à utiliser pour effectuer ces transformations sont rappelés dans le tableau 1 et ont été décrits dans [1] et [2].

Loi suivie par X_i	Programme à appliquer à l'échantillon uniforme de départ
Loi uniforme sur [0 ; 1]	Aucun
Loi uniforme sur [a ; b]	uniform.exe
Loi dérivée d'arc sinus	darcsin.exe
Loi normale	norm.exe
Loi triangle	triang.exe

Tableau 1
Conversion des lois

Enfin la création de la matrice des échantillons d'entrée est réalisée à l'aide du logiciel MkOutSpl (cf. §3.) qui procède à la création de l'échantillon de la grandeur de sortie. Par la suite différents traitements peuvent être effectués sur l'échantillon de sortie. Citons par exemple le calcul de sa moyenne avec le programme mean (§4) ou le calcul de son écart type avec le programme std2 (§5).

L'ensemble de ces logiciels qui constituent le Pack Monte-Carlo peuvent être téléchargés en annexe de ce dossier. Il est conseillé de tous les copier dans un répertoire de votre disque dur et de travailler directement dans ce répertoire en ligne de commande MS-DOS (fonction « Invite de commandes » sous Windows).

2. Création des sous-échantillons (Split.exe)

L'objectif est d'avoir p échantillons pour les p grandeurs d'entrées. D'autre part ces échantillons ne doivent pas être corrélés. Le moyen le plus simple pour y parvenir est de découper un échantillon initial de période la plus élevée possible et ne présentant pas d'autocorrélations. L'opération de découpage de l'échantillon en plusieurs sous-échantillons est réalisée à l'aide du logiciel split. Ce logiciel est utilisé en ligne de commande avec le paramétrage suivant :

split.exe fichier_source nombre_de_fichiers_a_creer

Le nombre d'échantillons à créer doit être un diviseur du nombre de valeurs dans le fichier source. Les fichiers créés sont nommés « nom_chrono.extension » (chrono commence à 1). Par exemple avec le paramétrage suivant :

split.exe file.txt 3

le fichier file.txt sera découpé en trois fichiers file_1.txt, file_2.txt et file_3.txt comme représenté sur la figure 2.

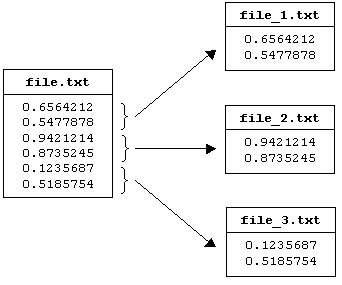
Fig. 2. - Création de sous échantillons

3. Génération de l'échantillon de sortie (MkOutSpl.exe)

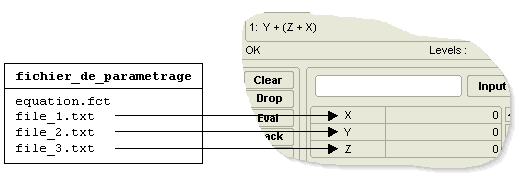
Cette étape consiste à évaluer le modèle de la mesure pour différentes réalisations de la variable aléatoire (X₁, ..., X_p). Cette opération est réalisée à partir du logiciel MkOutSpl. Ce logiciel est utilisé en ligne de commande avec le paramétrage suivant :

MkOutSpl.exe fichier_de_parametrage fichier_a_creer

le fichier de paramétrage contient :

en première ligne le nom du fichier correspondant à l'équation du modèle (équation programmée avec PFS-AC) [3] ;
les nom des fichiers avec les échantillons des grandeurs d'entrée (un fichier par ligne). Les fichiers sont saisis dans l'ordre d'apparition des variables sur PFS-AC (figure 3).

Fig. 3. - Position des échantillons dans le fichier de paramétrage

4. Calcul de la moyenne (Mean.exe)

Avec les méthodes de Monte-Carlo la taille des échantillons est telle qu'il est préférable de ne pas calculer les moyennes par les procédés habituels. En effet, la somme des valeurs sur des échantillons comportant plusieurs millions de valeurs peut rapidement dépasser les capacités du calculateur employé.

La méthode employée ici consiste à réduire successivement la taille de l'échantillon. Prenons par exemple un échantillon de n valeurs x₁, ..., x_n. On cherche k ∈ \( \mathbb{N} \) un diviseur de n, différent de 1 et n, pour lequel il existe un entier p tel que : n = k · p. On a alors :

\( \begin{eqnarray} \dfrac{x_{1}+\ldots + x_{\text{n}}}{n} = \dfrac{ \dfrac{x_{1}+\ldots + x_{\text{k}}}{k} + \dfrac{x_{\text{k}+1}+\ldots + x_{\text{2} \cdot \text{k}}}{k} + \ldots + \dfrac{x_{(\text{p}-1)\cdot \text{k}+1}+\ldots + x_{\text{n}}}{k} }{p} \end{eqnarray} \) .

(1)

En posant pour i ∈ [1 ; p] :

\( \begin{eqnarray} x_{\text{i},\text{k}} = \dfrac{x_{(\text{i}-1)\cdot \text{k}+1}+\ldots + x_{\text{i} \cdot \text{k}}}{k}\end{eqnarray} \) ,

(2)

l'équation (1) devient :

\( \begin{eqnarray} \dfrac{x_{1}+\ldots + x_{\text{n}}}{n} = \dfrac{x_{1,1}+\ldots + x_{1,\text{p}}}{p} \end{eqnarray} \) .

(3)

Le calcul de la moyenne de x₁, ..., x_n revient alors à calculer la moyenne du nouvel échantillon x_1,1, ..., x_1,p de taille p < n. On réitère ainsi l'opération jusqu'à obtenir un échantillon de taille compatible avec les possibilités de calcul de l'ordinateur employé (ou jusqu'à ce que n soit un nombre premier) comme indiqué sur la figure 4. L'implicite de cette remarque est qu'il est souhaitable que n puisse se décomposer facilement en un produit d'entiers (par exemple un nombre de la forme 10^m est idéal).

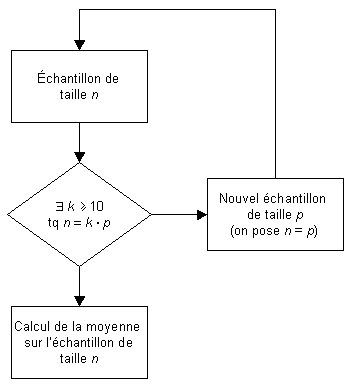
Fig. 4. - Algorithme utilisé pour le calcul de la moyenne.

Cette méthode de calcul est appliquée par le logiciel mean. Celui-ci s'utilise en mode ligne de commande en employant la syntaxe suivante :

mean.exe [-f] fichier_source

Dans ce code, -f est optionnel et indique s'il est présent qu'il faut créer un fichier au format texte contenant le résultat. Le cas échéant le fichier créé porte le nom mean.dat.

5. Calcul de l'écart type (Std2.exe)

De même que pour le calcul de la moyenne, le calcul de l'écart type pour des échantillons de très grande taille nécessite d'utiliser des méthodes spécifiques. Dans le cas présent le logiciel std2 utilise le logiciel mean (ce logiciel doit être dans le même répertoire que std2) pour évaluer l'écart type. La syntaxe à employer est la suivante :

std2.exe [-f] fichier_source

Dans ce code, -f est optionnel et indique s'il est présent qu'il faut créer un fichier au format texte contenant le résultat. Le cas échéant le fichier créé porte le nom std2.dat.

6. Création d'une statistique par classes (SplToBin.exe)

6.1. Méthode employée

Soit {x₁, ..., x_n} un échantillon de n réalisations d'une variable aléatoire X. Afin de simplifier le traitement de cet échantillon qui peut contenir plusieurs millions de valeurs, il est pratique de le transformer en une statistique par classes définie dans les lignes qui suivent.

Soient :

\( a \leqslant \min (x_{1}, \ldots x_{\text{n}}) \) ;

\( b \geqslant \max (x_{1}, \ldots x_{\text{n}}) \) ;

et K un entier non nul.

On pose : Δ = (b − a) / K .

A partir de ces notations on définit :

a_i = a + Δ · i , avec i ∈ [0 ; K] .

Soit {c_i}_{i ∈ [1,K ]} la suite d'intervalles définie par :

\( c_{\text{i}} = \begin{cases} [a_{\text{i}-1}~;~a_{\text{i}}[ & \text{pour} & i \in [1~;~K-1]~\text{,} \\[1ex] [a_{\text{i}-1}~;~a_{\text{i}}] & \text{pour} & i = K~\text{.} \end{cases} \)

La suite {c_i}_{i ∈ [1,K ]} est une partition de [a ; b]. Par la suite c_i sera appelé la i^e classe.

Pour i ∈ [1 ; K] on note n_i le nombre de valeurs de l'échantillon dans la classe c_i :

n_i = Card {x_p tq x_p ∈ c_i avec p ∈ [1 ; K]} .

La suite {c_i}_{i ∈ [1,K ]} est une statistique par classes de l'échantillon. Afin d'apporter une réelle simplification, il faudra que les classes ne soient pas trop petites, id trop nombreuses, mais qu'elles soient quand-même en nombre suffisant pour conserver l'essentiel de l'information initiale. Dans la pratique le nombre K est pris égal à quelques dizaines, au plus quelques centaines.

Pour constituer cette statistique, la méthode la plus rapide en terme de temps de calcul est de prélever successivement les valeurs de l'échantillon et d'incrémenter les valeurs de n_i correspondantes. Par exemple en prélevant la valeur x_p avec p ∈ [1 ; K] on incrémentera d'une unité la valeur de n_i dont l'indice i est calculé par la formule :

\( i = \begin{cases} \left\lfloor \dfrac{x - a}{\Delta} \right\rfloor + 1 & \text{si} & x_{\text{p}} < b~\text{,} \\[1ex] K & \text{si} & x_{\text{p}} = b~\text{.} \end{cases} \)

Dans cette expression, la notation \( \lfloor . \rfloor \) désigne la fonction qui retourne la partie entière sans arrondi (troncature).

6.2. Mise en pratique

La création de la statistique par classe est effectuée dans la pratique à l'aide du logiciel SplToBin. Ce logiciel s'utilise en ligne de commande avec le paramétrage suivant :

spltobin.exe [-ab] fichier_source fichier_destination a b n

avec :

fichier_source : le nom du fichier contenant l'échantillon de données ;
fichier_destination : le nom du fichier qui contiendra les classes et les effectifs ;
a : la valeur mini de l'intervalle (facultatif) ;
b : la valeur maxi de l'intervalle (facultatif) ;
n : le nombre de classes.

Les valeurs de a et b sont optionnelles. Par exemple :

Commande :
spltobin.exe source.txt dest.txt 10
Résultat :
Le logiciel calcule automatiquement les valeurs extrêmes à partir du fichier source.txt et crée 10 classes.

Commande :
spltobin.exe -a source.txt dest.txt 1 10
Résultat :
La valeur minimale est prise égale à 1. Le logiciel calcule automatiquement la valeur maximale à partir du fichier source.txt et crée 10 classes.

Commande :
spltobin.exe -b source.txt dest.txt 50 10
Résultat :
La valeur maximale est prise égale à 50. Le logiciel calcule automatiquement la valeur minimale à partir du fichier source.txt et crée 10 classes.

Commande :
spltobin.exe -ab source.txt dest.txt 1 50 10
Résultat :
La valeur minimale est prise égale à 1 et la valeur maximale est prise égale à 50. Le logiciel crée 10 classes.

Le fichier de sortie est au format texte et à la forme suivante :

«
	a₀	→	a₁	→	n₁	¶
	a₁	→	a₂	→	n₂	¶
	·	→	·	→	·	¶
	·	→	·	→	·	¶
	·	→	·	→	·	¶
	a_K−1	→	a_K	→	n_K	¶
»

Dans ce schéma, le caractère « → » désigne la marque de tabulation (caractère ASCII n° 009) et le caractère « ¶ » désigne un saut de ligne avec retour chariot.

Le logiciel ShowBin.exe permet de visualiser directement le fichier créé par SplToBin.exe (cf. fig. 5).

Fig. 5. - Utilisation de ShowBin.exe pour visualiser une statistique par classes.
L'exemple représente la distribution d'une loi dérivée de l'arc sinus
(échantillon de 1 million de points ; la barre bleue représente la moyenne calculée avec
mean.exe ; les barres rouges l'intervalle élargi à 95 % déterminé avec BinToCIS.exe).

7. Test des lois

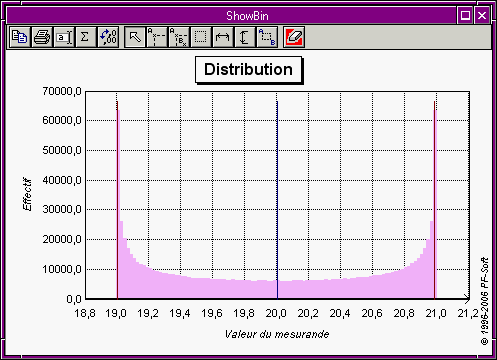
Lorsque l'on a un échantillon, il peut être intéressant de regarder dans quelle mesure il se rapproche d'une loi connue. Par exemple si on somme plusieurs fois des variables aléatoires indépendantes, on devra obtenir, d'après le théorème de la limite centrée, une loi convergeant vers une loi normale.

7.1. Le critérium de Pearson

Soit {x₁, ..., x_n} un échantillon de n réalisations d'une variable aléatoire X. Soit (c_i ; n_i)_i∈[1;K] une statistique de K classes de l'échantillon.

En reprenant les notations du paragraphe précédent les données se mettent sous la forme du tableau 2.

Classe n°	Limite de classe inférieure	Limite de classe supérieure	Effectif dans la classe
1	a₀	a₁	n₁
2	a₁	a₂	n₂
.	.	.	.
.	.	.	.
.	.	.	.
K	a_K-1	a_K	n_K

Tableau 2
Statistique par classes

On note N l'effectif de l'échantillon :

N = n₁ + n₂ + ... + n_K .

Supposons que la variable aléatoire X suive une loi de probabilité \( \mathscr{L} \). Dans ces conditions, pour i ∈ [1 ; K], la probabilité qu'une valeur soit dans la classe c_i vaut :

p_i = Pr (a_i−1 < X < a_i) ,

et donc l'effectif théorique de cette classe devrait être :

t_i = p_i × N .

On complète donc le tableau 2 avec les effectifs théoriques pour obtenir le tableau 3.

Classe n°	Limite de classe inférieure	Limite de classe supérieure	Effectif dans la classe	Effectif théorique dans la classe
1	a₀	a₁	n₁	t₁
2	a₁	a₂	n₂	t₂
.	.	.	.	.
.	.	.	.	.
.	.	.	.	.
K	a_K-1	a_K	n_K	t_K

Tableau 3
Statistique par classes et effectifs théoriques

On définit l'indice de divergence s par :

\( \begin{eqnarray} s = \sum_{\text{i}=1}^{\text{K}} \dfrac{ (n_{\text{i}} - t_{\text{i}})^{2} }{ t_{\text{i}} } \end{eqnarray} \) .

D'après le théorème de Pearson, la distribution de s suit une loi du \( \chi^{2} \) (khi deux) à K − 1 degrés de liberté. Sur la figure 6 l'allure de cette distribution a été représentée : la surface hachurée en vert représente la probabilité d'une valeur inférieure à x. Pour une valeur x suffisamment élevée, la probabilité que s soit inférieur à cette valeur est élevée. En d'autre terme, si s est supérieur à cette valeur on considérera que cela est très improbable, et que X ne suit pas la loi \( \mathscr{L} \). En revanche si s est inférieur à cette valeur cela ne voudra pas nécessairement dire que X suit la loi \( \mathscr{L} \), mais simplement que l'hypothèse que X suit la loi \( \mathscr{L} \) n'est pas contredite.

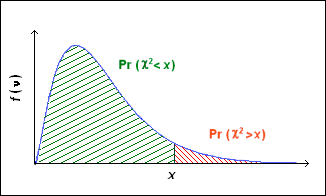
Fig. 6. - Densité de probabilité de la loi du \( \chi^{2} \)

Remarque : la valeur \( \text{Pr}~(\chi^{2} \leqslant x) \) correspond à la fonction KHI2(.;.) sur PFS-AC [3].

7.2. Test d'une loi uniforme (IsUnfrm.exe)

Par exemple après avoir généré un échantillon de 5 millions de points avec u82 et créé une statistique par classes avec le logiciel SplToBin nous avons les données reproduites dans le tableau 4. L'effectif théorique étant égal à l'effectif total multiplié par la probabilité p_i d'avoir une valeur dans la classe c_i. En reprenant les notations du §6, p_i = (b − a) / K.

Classe n°	Limite de classe inférieure	Limite de classe supérieure	Effectif dans la classe	Effectif théorique dans la classe
1	0,0	0,1	499 778	500 000
2	0,1	0,2	500 240	500 000
3	0,2	0,3	499 872	500 000
4	0,3	0,4	500 242	500 000
5	0,4	0,5	499 961	500 000
6	0,5	0,6	499 045	500 000
7	0,6	0,7	499 928	500 000
8	0,7	0,8	499 869	500 000
9	0,8	0,9	500 504	500 000
10	0,9	1,0	500 561	500 000

Tableau 4
Statistique par classes et effectifs théoriques

A partir de ces données, on calcule un indice de divergence valant :

s = 3,37 .

Le calcul du fractile de la loi du \( \chi^{2} \) pour 9 degrés de liberté et une probabilité de 95 % donne avec le logiciel PFS-AC [3] (« FKHI2(9 ; 0.95) ») :

x = 16,92 .

Comme \( s \leqslant x \), l'hypothèse selon laquelle l'échantillon provient d'une variable aléatoire de loi uniforme sur [0 ; 1] n'est pas contredite.

Ce calcul étant quelque peu fastidieux, il est possible de faire automatiquement le test avec le logiciel IsUnfrm.exe comme indiqué sur la figure 7.

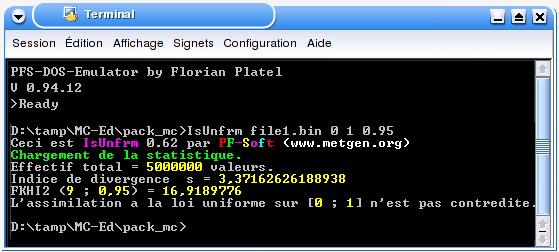
Fig. 7. - Test automatisé d'une loi uniforme

7.3. Test d'une loi normale (IsNorm.exe)

Par exemple après avoir généré un échantillon de 5 millions de points avec u82, puis transformé cet échantillon avec norm (moyenne m =20 ; écart type s = 0,2) et créé une statistique par classes avec le logiciel SplToBin nous avons les données reproduites dans le tableau 5. L'effectif théorique étant égal à l'effectif total multiplié par la probabilité p_i d'avoir une valeur dans la classe c_i. En reprenant les notations du §6, la probabilité p_i est obtenue par la formule :

p_i = NORM (m, σ, a_i) − NORM (m, σ, a_i−1) ,

avec NORM (m, σ, x) la fonction du logiciel PFS-AC [3] ; donnant la probabilité pour une variable suivant la loi normale N(m, σ) d'être inférieure à x.

Classe n°	Limite de classe inférieure	Limite de classe supérieure	Effectif dans la classe	Effectif théorique dans la classe
1	18,80	19,04	8	3,96
2	19,04	19,28	813	791,58
3	19,28	19,52	40 611	40 192,14
4	19,52	19,76	535 652	534 360,67
5	19,76	20,00	1 924 260	1 924 651,65
6	20,00	20,24	1 924 612	1 924 651,65
7	20,24	20,48	533 290	534 360,67
8	20,48	20,72	39 949	40 192,14
9	20,72	20,96	801	791,58
10	20,96	21,20	4	3,96

Tableau 5
Statistique par classes et effectifs théoriques

A partir de ces données, on calcule un indice de divergence valant :

s = 15,99 .

Le calcul du fractile de la loi du \( \chi^{2} \) pour 9 degrés de liberté et une probabilité de 95 % donne avec le logiciel PFS-AC [3] (« FKHI2(9 ; 0.95) ») :

x = 16,92 .

Comme \( s \leqslant x \), l'hypothèse selon laquelle l'échantillon provient d'une variable aléatoire de loi normale de moyenne m = 20 et d'écart type σ = 0,2 n'est pas contredite.

Ce calcul étant quelque peu fastidieux, il est possible de faire automatiquement le test avec le logiciel IsNorm.exe comme indiqué sur la figure 8.

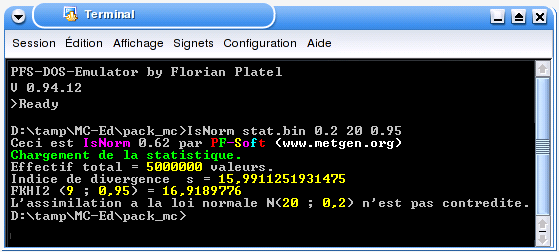
Fig. 8. - Test automatisé d'une loi normale

8. Détermination de la fonction de répartition (BinToCdf.exe)

Soit X une variable aléatoire. On définit la fonction de répartition de X souvent notée G :

\( \begin{array}{l} G : & \mathbb{R} & \to & [0~;~1] \\ & x & \mapsto & P(X < x) \end{array} \)

Disposant d'une statistique par classes, il est aisé d'obtenir une approximation \( \hat{G} \) de \( G \) de manière discrète. Dans la pratique, la variable endogène sera prise égale au centre des classes et la variable exogène correspondra à l'effectif cumulé divisé par l'effectif total. Le principe de calcul est résumé sur la figure 9 en adoptant les notations définies au paragraphe 6.1.

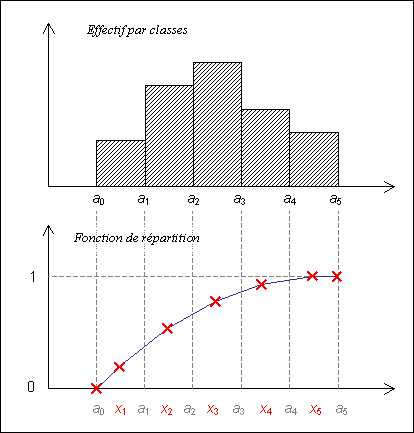
Fig. 9. - Approximation de la fonction de répartition
à partir d'une statistique par classes

Autrement dit, pour i ∈ [1 ; K], on a :

\( \begin{eqnarray} x_{\text{i}} = \dfrac{\left(a_{\text{i}} + a_{\text{i}-1}\right)}{2} \end{eqnarray} \) et \( \begin{eqnarray} \hat{G}(x_{\text{i}}) = \dfrac{1}{N} \cdot \sum_{\text{k}=1}^{\text{i}} n_{\text{k}} \end{eqnarray} \) .

Pour assurer la couverture de tout l'intervalle on pose pour la borne inférieure :

\( x_{0} = a_{0} \) et \( \hat{G}(x_{0}) = 0 \) ,

et pour la borne supérieure :

\( x_{\text{K}+1} = a_{\text{K}} \) et \( \hat{G}(x_{\text{K}+1}) = 1 \) .

On a ainsi défini \( \hat{G} \) de manière discrète sur un ensemble de K + 2 points couvrant l'intervalle où la fonction de répartition passe de 0 à 1.

Ce calcul peut être effectué automatiquement à partir du logiciel BinToCdf.exe qui transforme une statistique par classes en une fonction de répartition. Le fichier résultat est au format texte et contient les données suivantes :

«
	x₀	→	G(x₀)	¶
	x₁	→	G(x₁)	¶
	·	→	·	¶
	·	→	·	¶
	·	→	·	¶
	x_K+1	→	G(x_K+1)	¶
»

Dans ce schéma, le caractère « → » désigne la marque de tabulation (caractère ASCII n° 009) et le caractère « ¶ » désigne un saut de ligne avec retour chariot.

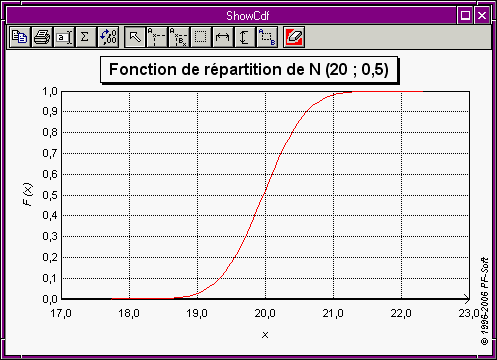
Le logiciel ShowCdf.exe permet de visualiser directement le fichier créé par BinToCdf.exe (cf. fig. 10).

Fig. 10. - Utilisation de ShowCdf pour visualiser
une fonction de répartition.

9. Détermination de l'intervalle élargi

A l'issue de la simulation selon la méthode Monte-Carlo, on dispose d'un échantillon de valeurs de la grandeur de sortie. Pour que la méthode prenne tout son intérêt il s'agit d'être capable d'indiquer un intervalle dans lequel la probabilité de trouver une valeur est élevée. En d'autre termes il s'agit de déterminer un intervalle contenant une proportion p ∈ ]0 ; 1[ de valeurs.

Tout d'abord, nous avons vu dans §6 et §8 qu'il est possible de transformer l'échantillon en une approximation de la fonction de répartition notée \( \hat{G} \). Soit α ∈ [0 ; 1 − p].

9.1. Cas d'une distribution asymétrique (CdfToCi.exe)

Par définition de la fonction de répartition, l'intervalle \( \left[ \hat{G}\,^{-1}(\alpha)~;\hat{G}\,^{-1}(\alpha + p) \right] \) contient une proportion p de valeurs (cf. fig. 11).

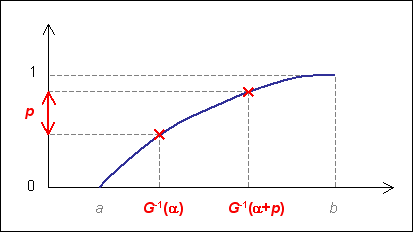
Fig. 11. - Détermination de l'intervalle élargi
à partir de la fonction de répartition

Bien évidemment, si p est différent de 1, il existe une infinité d'intervalles. Le supplément du GUM [4] apporte la réponse en préconisant de retenir l'intervalle le plus court. C'est à dire l'intervalle \( \left[ \hat{G}\,^{-1}(\alpha)~;\hat{G}\,^{-1}(\alpha + p) \right] \) avec α la valeur minimisant la fonction :

\( \begin{array}{l} \Delta : & ]0~;~1 - p[ & \to & \mathbb{R} \\ & x & \mapsto & \hat{G}\,^{-1}(x + p) - \hat{G}\,^{-1}(x) \end{array} \) .

Ce calcul peut être effectué automatiquement à partir du logiciel CdfToCi.exe qui détermine l'intervalle élargi contenant une proportion p de valeurs à partir du fichier de la fonction de répartition.

L'application de cette méthode n'est pas toujours très heureuse, par exemple une infinité d'intervalles conviennent dans le cas d'une loi uniforme. Ainsi dans ce cas, le logiciel fournira un intervalle qui ne sera pas forcément le bon. Cette remarque souligne la nécessité de toujours représenter graphiquement l'histogramme des distribution (par exemple avec le logiciel ShowBin.exe) et de repérer l'intervalle visuellement pour déceler d'éventuelles anomalies.

Par exemple dans le cas de la distribution uniforme il faut utiliser la méthode applicable aux distributions symétriques.

9.2. Cas d'une distribution symétrique (CdfToCiS.exe)

Dans ce cas de figure la détermination est très rapide puisque l'intervalle élargi est :

\( \begin{eqnarray} \left[ \hat{G}\,^{-1}\left( \dfrac{1 - p }{2} \right)~;~\hat{G}\,^{-1}\left( \dfrac{1 + p}{2} \right) \right] \end{eqnarray} \) .

Ce calcul peut être effectué automatiquement à partir du logiciel CdfToCiS.exe qui détermine l'intervalle élargi contenant une proportion p de valeurs à partir du fichier de la fonction de répartition dans le cas d'une distribution symétrique.

10. Exemples de calcul : étalonnage d'une masse

L'exemple qui suit est extrait de [4]. Ce choix a été effectué pour valider les calculs réalisés avec le Pack Monte-Carlo.

Soit l'étalonnage d'une masse W par comparaison avec une masse R. Le modèle de la mesure extrait de [4] est :

\( \begin{eqnarray} m_{\text{W}, \text{C}} = \left( m_{\text{R}, \text{C}} + \delta m_{\text{R}, \text{C}} \right) \cdot \left[ 1 + \left( a - a_{0} \right) \cdot \left( \dfrac{1}{\rho_{\text{W}}} - \dfrac{1}{\rho_{\text{R}}} \right) \right] \end{eqnarray} \) ,

avec :

m_W,C	:	la valeur de la masse à déterminer (en valeur conventionnelle) ;
m_R,C	:	la valeur de la masse de référence (en valeur conventionnelle) ;
δm_R,C	:	la valeur des masses de référence additionnelles pour équilibrer la balance (en valeur conventionnelle ;
a	:	la valeur de la masse volumique de l'air ;
a₀	:	la valeur la masse volumique « conventionnelle » (connue exactement et vaut 1,2 kg/m³) ;
ρ_W	:	la valeur de la masse volumique de W ;
ρ_R	:	la valeur de la masse volumique de R.

Dans les lignes qui suivent nous allons étudier l'écart E à la valeur nominale (en mg), soit :

E = m_W,C − 10⁵ .

Concernant les grandeurs d'entrée, on utilise les données du tableau 6 extraites de [4] :

X_i	Loi	Moyenne	Ecart type	Demi intervalle
m_R,C	Normale	10⁵ mg	0,050 mg	/
δm_R,C	Normale	1,234 mg	0,020 mg	/
a	Uniforme	1,20 kg/m³	/	0,10 kg/m³
ρ_W	Uniforme	8 000 kg/m³	/	1 000 kg/m³
ρ_R	Uniforme	8 000 kg/m³	/	50 kg/m³

Tableau 6
Définition des lois des grandeurs d'entrée

Afin de simplifier les calculs, compte tenu des rapports des grandeurs dans l'équation, les masses seront exprimées en mg et les masses volumiques en kg/m³.

L'équation PFS-AC [3] a été nomée cal_mass.fct. La séquence de commandes reproduite dans le tableau 7 a été effectuée.

Commande	Résultat
u82 0.spl 5000000	Création d'un échantillon de 5 millions de valeurs (fichier : 0.spl)
split 0.spl 5	Création de 5 sous échantillons contenant chacun 1 million de valeurs (fichiers : 0_1.spl à 0_5.spl)
norm 0.05 1E5 0_1.spl 1.spl	Création de l'échantillon de m_R,C (fichier : 1.spl)
norm 0.02 1.234 0_2.spl 2.spl	Création de l'échantillon de δm_R,C (fichier : 2.spl)
uniform 0.10 1.20 0_3.spl 3.spl	Création de l'échantillon de a (fichier : 3.spl)
uniform 1000 8000 0_4.spl 4.spl	Création de l'échantillon de ρ_W (fichier : 4.spl)
uniform 50 8000 0_5.spl 5.spl	Création de l'échantillon de ρ_R (fichier : 5.spl)
mkoutspl param.txt y.spl	Création de l'échantillon de la grandeur de sortie. Le fichier param.txt contient : « cal_mass.fct¶ 1.spl¶ 2.spl¶ 3.spl¶ 4.spl¶ 5.spl¶ » Le fichier créé est : y.spl.
spltobin y.spl y.bin 100	Création d'une statistique par classes : 100 classes ; fichier y.bin
bintocdf y.bin y.cdf	Création de la fonction de répartition : fichier y.cdf
mean y.spl	La moyenne vaut 1,233 9 mg
std2 y.spl	L'écart type vaut 0,075 5 mg
cdftocis y.cdf 0.95	L'intervalle élargi est [1,080 5 mg ; 1,380 0 mg]
showbin -cm y.bin 1.0805 1.3800 1.2339	Affichage de la distribution avec l'intervalle élargi et la moyenne (figure 12).

Tableau 7
Séquence des commandes

A l'issue de ces calculs on a les résultats suivants :

moyenne : 1,234 mg ;
écart type : 0,076 mg ;
intervalle élargi : [1,080 mg ; 1,381 mg].

Ces résultat sont reproduits sur la figure 12.

Fig. 12. - Résultat de l'étalonnage

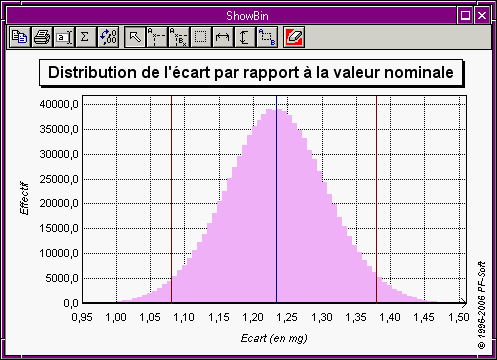
En utilisant la loi de propagation des variances on aurait trouvé (le détail des calculs effectués sur Gumy est reproduit dans le tableau 8 :

moyenne : 1,234 mg ;
écart type : 0,054 mg ;
intervalle élargi : [1,126 mg ; 1,342 mg].

Tableau 8
Calcul en utilisant la loi de propagation des variances

Dans ce cas, utiliser la loi de propagation des variances revient à sous-estimer l'incertitude. On démontre dans [4] qu'en développant la loi de propagation des variances à l'ordre 2 on obtient une incertitude voisine de celle obtenue par la méthode de Monte-Carlo.

11. Distribution provenant d'un calcul de Monte-Carlo (CdfToSpl.exe)

11.1. Méthode employée

D'après [4] à l'issue d'un calcul d'incertitudes effectué en propageant les distribution, il est possible de récupérer le résultat de la simulation de Monte-Carlo et de l'injecter dans un autre calcul. La mise en oeuvre de cette idée nécessite toutefois quelques précautions.

Supposons par exemple qu'une grandeur Y est obtenue à partir de n grandeurs d'entrée {X₁, ..., X_n} du modèle de la mesure f :

Y = f (X₁, ..., X_n) ,

et qu'une grandeur T est obtenue à partir des grandeurs d'entrée {Z₁, ..., Z_p, Y} du modèle de la mesure h :

T = h (Z₁, ..., Z_p, Y) .

Après avoir généré un échantillon de la grandeur Y, on pourrait être tenté de récupérer cet échantillon et de l'injecter directement dans h pour générer un échantillon de T. Cela serait extrêmement risqué puisqu'à la base l'échantillon uniforme qui aura servi à générer les échantillons de X₁, ..., X_n et donc celui de Y sera le même que celui qui servira à générer les échantillons de Z₁, ..., Z_p (cf. fig. 13). En d'autres termes, les échantillons de Z₁, ..., Z_p et de Y seront très certainement corrélés.

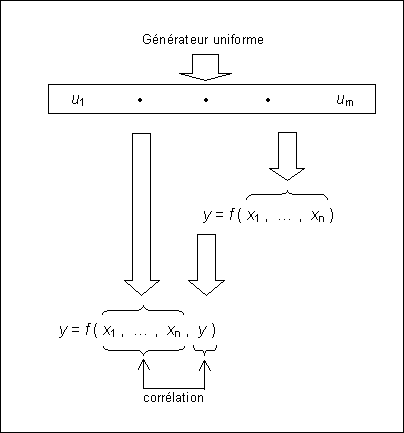
Fig. 13. - Risque de corrélation en récupérant directement l'échantillon
d'une simulation de Monte-Carlo

Afin de contourner ce risque de corrélation, la méthode la plus robuste est de générer un échantillon de Y en même temps que les échantillons de Z₁ à Z_p, ce qui revient à créer un générateur de nombres aléatoires suivant la loi de Y.

On a vu dans les chapitres qui précèdent q'il est possible de créer une approximation de la fonction de répartition à partir d'un échantillon. Soit \( \hat{G}\,^{-1}(Y) \) la fonction de répartition approchée construite à partir de l'échantillon de Y déduit de f (X₁, ..., X_n) par la méthode de Monte-Carlo.

En appliquant la méthode de la transformation réciproque [2] à \( \hat{G}_{\text{Y}} \) on est capable de créer un générateur de nombres aléatoires selon la loi de Y. En d'autres termes, on crée un générateur tel que uniform, darcsin, norm, triang ([1] et [2]) qui sera directement appliqué à l'échantillon uniforme utilisé pour générer Z₁, ..., Z_p. Donc le problème de la corrélation ne se pose plus.

Dans la pratique, les temps de calculs peuvent être extrêmement long (en particulier pour rechercher l'intervalle sur lequel effectuer l'interpolation). Afin de réduire les temps de calculs, la fonction de répartition sera simplifiée comme indiqué sur la figure 14 en espaçant régulièrement les points de définition entre 0 et 1.

Fig. 14. - Reconstruction de la fonction de répartition.
La fonction de répartition approchée est représentée en bleu.
La fonction reconstruite est représentée en rouge.

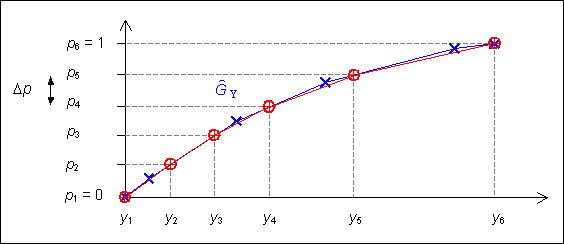
Supposons que la fonction de répartition approchée est définie à l'aide de N points. On divise alors l'intervalle [0 ; 1] en N sous intervalles de longueur : Δp = 1 / (N − 1). Soit i ∈ {1, ..., N}. On défini : p_i = (i − 1) · Δp. A chaque valeur p_i, on associe \( y_{\text{i}} = \hat{G}\,^{-1}(p_{\text{i}}) \) que l'on stocke dans un tableau.

L'algorithme de calcul est alors le suivant :

on lit r ∈[0 ; 1] dans l'échantillon uniforme de départ ;
on calcule i = [r / Δp] + 1 , avec [.] la fonction renvoyant la partie entière ;
la valeur de la réciproque est : y_i = (r − p_i) / Δp · (y_i+1 - y_i) .

Cet algorithme a été mis en oeuvre dans le programme CdfToSpl.exe figurant dans le Pack Monte-Carlo.

11.2. Exemple d'application

A l'aide des générateurs u82 [1] et norm [2] on a généré un échantillon de 5 millions de valeurs suivant une loi normale de moyenne valant 10 et d'écart type valant 1. A partir ce cet échantillon on a créé une statistique par classes (500 classes) à l'aide de SplToBin, puis on a transformé cette statistique par classes en fonction de répartition à l'aide de BinToCdf. Cette fonction de répartition a ensuite été utilisée par CdfToSpl pour générer un nouvel échantillon de 5 millions de valeurs. Les deux distributions obtenues sont représentées sur la figure 15.

Fig. 15. - Comparaison entre la distribution originale et la densité reconstruite par CdfToSpl.
La courbe du haut représente la densité originale d'une loi normale de moyenne 10 et
d'écart type valant 1. La courbe du bas représente la densité reconstruite par CdfToSpl.
On remarque que les deux courbes diffèrent principalement aux points extrêmes
(au dessus de 13 et en dessous de 7). Les lignes en bleu et en rouge représentent
respectivement la moyenne et l'intervalle élargi calculés pour chacune des distribution.

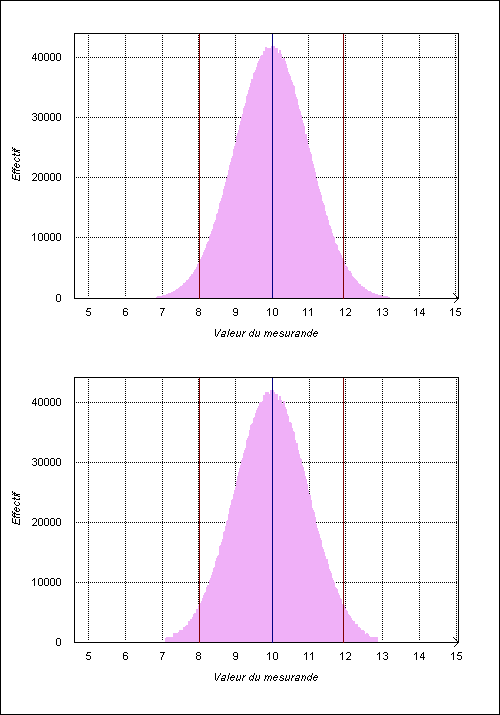
Le calcul de la moyenne, de l'écart type et de l'intervalle élargi à 95 % a été effectué sur les deux distributions. Les résultats sont reportés dans le tableau 8.

Echantillon	Moyenne	Ecart type	Intervalle élargi	Test du χ²
Echantillon initial	9,998 82	1,000 22	[8,027 ; 11,948]	Oui
Echantillon reconstruit par CdfToSpl	9,988 21	1,013 82	[8,016 ; 11,938]	Non

Tableau 8
Comparaison des échantillons

Sur cet exemple on constate une dégradation, qui reste cependant négligeable devant l'écart type. L'échec du test du χ² s'explique principalement par les points extrêmes (cf. fig. 15).

12. Calculs externes vs calculs internes

On parle ici de calculs externes lorsque la taille des échantillons est trop importante pour qu'ils soient stockés en mémoire. Inversement lorsque les échantillons sont chargés en mémoire on parle de calculs internes. Il n'y a pas de règle pour prédéfinir une taille d'échantillons. Le supplément du Gum [4] conseille toutefois des échantillons avec un million de points. De façon générale l'occupation mémoire est un problème important avec la méthode de Monte-Carlo. La stratégie qui a consisté à développer ici des programmes fonctionnant en mode console permet de réaliser des programmes rapides, très peu consommateurs d'espace mémoire. Ceux-ci génèrent directement des échantillons de points sous la forme de fichiers au format texte sur le disque dur (calculs externes). Enfin le codage des compteurs du nombre de points a été effectué selon une méthode originale qui permet de créer des entiers comportant jusqu'à 255 chiffres : soit 10²⁵⁵ − 1 valeurs... En d'autres termes la limitation des échantillons proviendra vraisemblablement de la taille limite des fichiers supportés par votre machine : à titre d'illustration, un fichier de 10 millions de valeurs (comportant 15 décimales) d'une loi U([0 ; 1]) occupe en moyenne 180 Mo.

13. Perspectives...

Il reste maintenant à créer une interface graphique permettant de piloter l'ensemble des modules du Pack Monte-Carlo fonctionnant en ligne de commande.

ANNEXE
Modules de calcul du Pack Monte-Carlo

Nom	Utilisation
bintocdf.exe	Création de la fonction de répartition à partir d'une statistique par classes
cdftoci.exe	Détermination de l'intervalle élargi à partir de la fonction de répartition (distribution asymétrique)
cdftocis.exe	Détermination de l'intervalle élargi à partir de la fonction de répartition (distribution symétrique)
cdftospl.exe	Génération d'un échantillon à partir d'une fonction de répartition.
darcsin.exe	Création d'un échantillon suivant la loi dérivée de l'arc sinus
distrib.exe	Représentation de la distribution d'un échantillon
isnorm.exe	Test du χ² selon la loi normale
isunfrm.exe	Test du χ² selon la loi uniforme
mean.exe	Moyenne d'un échantillon
mkoutspl.exe	Calcul de l'échantillon de sortie
norm.exe	Création d'un échantillon suivant la loi normale
pareto.exe	Création d'un échantillon suivant la loi de Pareto
showbin.exe	Visualisation d'une statistique par classes
showcdf.exe	Visualisation d'une fonction de répartition
split.exe	Découpage d'un échantillon
spltobin.exe	Création d'une statistique par classes à partir d'un échantillon
std2.exe	Calcul de l'écart type d'un échantillon
triang.exe	Création d'un échantillon suivant la loi triangle
u51.exe	Création d'un échantillon suivant la loi uniforme
u69.exe	Création d'un échantillon suivant la loi uniforme
u82.exe	Création d'un échantillon suivant la loi uniforme
uniform.exe	Création d'un échantillon suivant la loi uniforme

Télécharger le Pack Monte-Carlo

Références

[1]	PLATEL F., « Génération de nombres aléatoires pour la méthode de Monte-Carlo », MetGen, Dossier métrologie 21.
[2]	PLATEL F., « Quelques générateurs de nombres aléatoires pour la méthode de Monte-Carlo correspondant à des lois utilisées en métrologie », MetGen, Dossier métrologie 23.
[3]	PLATEL F., « Calcul symbolique sur ordinateur - Projet PFS-Algebraic Calculator », MetGen, Dossier divers 2.
[4]	JCGM, "Evaluation of measurement data - Supplement 1 to the "Guide to the expression of uncertainty in measurement" - Propagation of distributions using a Monte-Carlo method", BIPM, JCGM 101:2008, 2008, www.bipm.org.