
 |
Dans la pratique les instruments de mesure sont constitués d'un capteur et d'un afficheur séparé. C'est par exemple le cas d'une chaîne de température composée d'une sonde de température de type thermocouple et d'un indicateur séparé. Concernant l'étalonnage d'un tel dispositif, deux solutions se présentent :
En reprenant l'exemple précédent de la chaîne de température :
L'étalonnage en chaîne complète présente l'avantage de la simplicité :
Ceci étant, l'inconvénient de cette méthode est qu'il n'y a pas d'interchangeabilité des éléments de la chaîne. Par exemple si la sonde de température tombe en panne et qu'on la remplace, il faudra alors étalonner à nouveau la chaîne complète. Cela n'est pas toujours faisable en milieu de production (problèmes d'accessibilité des équipements dans un atelier de production, immobilisation des équipements entraînant l'arrêt des productions, ...). En revanche si les éléments sont étalonnés séparément, il suffit alors de remplacer la sonde par une nouvelle sonde qui aura été étalonnée au préalable en laboratoire. Donc pas d'intervention complexe en atelier nécessitant de déplacer un bain ou un four thermostatique, et, pas d'immobilisation de l'équipement de production. D'autre part, l'étalonnage périodique de l'afficheur qui est souvent lié à la machine de production, sera fait par simulation électrique avec un calibreur portatif, ce qui est une intervention généralement très rapide (de l'ordre de quelques minutes) pouvant par exemple être planifiée pendant un changement d'équipe.
Bien que la méthode de l'étalonnage séparé des différents maillons des chaînes de mesure soit très largement utilisée en milieu de production, il n'y a pas de publication concernant l'exploitation des données des étalonnages. Cette lacune est réparée dans les lignes qui suivent...
2. Etalonnage d'une chaîne de mesure par maillons séparés et exploitation des résultats
Soit une chaîne de mesure constituée d'un capteur (C) et d'un indicateur (I).
L'étalonnage consiste à appliquer une grandeur de référence (GC) au capteur et à mesurer le signal délivré par le capteur (SC). Dans la pratique GC et SC s'expriment dans des unités différentes. D'autre part, l'étalonnage devra mentionner l'incertitude sur la grandeur de référence et l'incertitude sur le signal délivré. On obtiendra donc une table d'étalonnage ayant la forme du tableau 1.
| Valeur étalon (GC) | Incertitude sur GC | Signal délivré (SC) | Incertitude sur SC |
| gc1 | u(gc1) | sc1 | u(sc1) |
| gc2 | u(gc2) | sc2 | u(sc2) |
| . | . | . | . |
| . | . | . | . |
| . | . | . | . |
| gcn | u(gcn) | scn | u(scn) |
2.2. Etalonnage de l'indicateur
L'étalonnage consiste à appliquer une grandeur de référence (GI) à l'indicateur et à lire l'affichage de l'indicateur (LI). Dans la pratique GI et LI s'expriment dans des unités différentes. L'unité de GI est la même que celle de la grandeur SC. De même que précédement, l'étalonnage devra mentionner l'incertitude sur la grandeur de référence et l'incertitude sur l'indication correspondante. On obtiendra donc une table d'étalonnage ayant la forme du tableau 2.
| Valeur étalon (GI) | Incertitude sur GI | Indication (LI) | Incertitude sur LI |
| gi1 | u(gi1) | li1 | u(li1) |
| gi2 | u(gi2) | li2 | u(li2) |
| . | . | . | . |
| . | . | . | . |
| . | . | . | . |
| gim | u(gim) | lim | u(lim) |
Remarque 1 : dans la pratique, le nombre de points d'étalonnage n et m ne sont pas forcément identiques, et, les points d'étalonnage ne coïncident pas forcément.
Remarque 2 : la plupart du temps les informations figurant dans les tableaux 1 et 2 ne sont pas proposés en standard dans les prestations d'étalonnage. Comme il est ridicule de payer pour des prestations inexploitables, il faut demander ces informations aux prestataires en métrologie lors de la revue de contrat.
Remarque 3 : pour le coté anecdotique on trouvera dans le lien suivant un exemple de certificat d'étalonnage produit par la société LCAL qui est tout à fait exemplaire de clarté et de concision. Celui-ci prouve que l'on peut faire une prestation de qualité, utile, sans surcroît de travail. Cela est d'autant plus remarquable que ce certificat date de 1985, date à laquelle le concept d'incertitude que l'on connaît aujourd'hui était encore naissant.
2.3. Calcul de la correction d'étalonnage de la chaîne complète
Soit li la valeur indiquée sur l'indicateur. Par interpolation à partir du tableau 2 on détermine la valeur du signal gi correspondante qui est appliquée aux bornes de l'indicateur. Puis à partir du tableau 1 on déduit par interpolation la valeur de la grandeur gc appliquée au capteur, qui correspond à un signal valant gi. La valeur de la correction vaut alors : c = gc − li.
Soit k ∈ [1 ; m] et tel que lik ≤ li < lik+1, on a alors :
| \( \begin{eqnarray} gi = \dfrac{ li - li_{\text{k}} }{ li_{\text{k} + 1} - li_{\text{k}} } \cdot (gi_{\text{k} + 1} - gi_{\text{k}}) + gi_{\text{k}} \end{eqnarray} \) . |
Soit p ∈ [1 ; n] et tel que scp ≤ gi < scp+1, on a alors :
| \( \begin{eqnarray} gc = \dfrac{ gi - sc_{\text{p}} }{ sc_{\text{p} + 1} - sc_{\text{p}} } \cdot (gc_{\text{p} + 1} - gc_{\text{p}}) + gc_{\text{p}} \end{eqnarray} \) . |
Donc :
| \( \begin{eqnarray} gc = \dfrac{ (li - li_{\text{k}}) \cdot (gi_{\text{k} + 1} - gi_{\text{k}}) + (gi_{\text{k}} - sc_{\text{p}}) \cdot (li_{\text{k} + 1} - li_{\text{k}}) }{ (li_{\text{k} + 1} - li_{\text{k}}) \cdot (sc_{\text{p} + 1} - sc_{\text{p}}) } \cdot (gc_{\text{p} + 1} - gc_{\text{p}}) + gc_{\text{p}} \end{eqnarray} \) , |
et finalement la correction vaut :
| \( \begin{eqnarray} gc = \dfrac{ (li - li_{\text{k}}) \cdot (gi_{\text{k} + 1} - gi_{\text{k}}) + (gi_{\text{k}} - sc_{\text{p}}) \cdot (li_{\text{k} + 1} - li_{\text{k}}) }{ (li_{\text{k} + 1} - li_{\text{k}}) \cdot (sc_{\text{p} + 1} - sc_{\text{p}}) } \cdot (gc_{\text{p} + 1} - gc_{\text{p}}) + gc_{\text{p}} - li \end{eqnarray} \) . | (1) |
2.4. Evaluation de l'incertitude sur la correction
En appliquant la loi de propagation des variances, la relation (1) donne :
| \(\begin{equation}\begin{split} u^{2}(c) = & \left( \dfrac{ \partial c}{ \partial li} \right)^{2} \cdot u^{2}(li) + \left( \dfrac{ \partial c}{ \partial gi_{\text{k}}} \right)^{2} \cdot u^{2}(gi_{\text{k}}) + \left( \dfrac{ \partial c}{ \partial gi_{\text{k}+1}} \right)^{2} \cdot u^{2}(gi_{\text{k}+1}) + \left( \dfrac{ \partial c}{ \partial li_{\text{k}}} \right)^{2} \cdot u^{2}(li_{\text{k}}) + \left( \dfrac{ \partial c}{ \partial li_{\text{k}+1}} \right)^{2} \cdot u^{2}(li_{\text{k}+1}) \\ & + \left( \dfrac{ \partial c}{ \partial gc_{\text{p}}} \right)^{2} \cdot u^{2}(gc_{\text{p}}) + \left( \dfrac{ \partial c}{ \partial gc_{\text{p}+1}} \right)^{2} \cdot u^{2}(gc_{\text{p}+1}) + \left( \dfrac{ \partial c}{ \partial sc_{\text{p}}} \right)^{2} \cdot u^{2}(sc_{\text{p}}) + \left( \dfrac{ \partial c}{ \partial sc_{\text{p}+1}} \right)^{2} \cdot u^{2}(sc_{\text{p}+1}) \end{split}\end{equation}\) |
avec les dérivées partielles :
| \(\begin{array}{l} \dfrac{ \partial c}{ \partial li} = \dfrac{ (gi_{\text{k}+1} -gi_{\text{k}}) \cdot (gc_{\text{p}+1} - gc_{\text{p}}) }{ (li_{\text{k}+1} - li_{\text{k}}) \cdot (sc_{\text{p}+1} - sc_{\text{p}}) } - 1 \\ \dfrac{ \partial c}{ \partial gi_{\text{k}}} = \dfrac{ (li_{\text{k}+1} - li) \cdot (gc_{\text{p}+1} - gc_{\text{p}}) }{ (li_{\text{k}+1} - li_{\text{k}}) \cdot (sc_{\text{p}+1} - sc_{\text{p}}) } \\ \dfrac{ \partial c}{ \partial gi_{\text{k}+1}} = \dfrac{ (li - li_{\text{k}}) \cdot (gc_{\text{p}+1} - gc_{\text{p}}) }{ (li_{\text{k}+1} - li_{\text{k}}) \cdot (sc_{\text{p}+1} - sc_{\text{p}}) } \\ \dfrac{ \partial c}{ \partial li_{\text{k}}} = \dfrac{ (li - li_{\text{k}+1}) \cdot (gi_{\text{k}+1} - gi_{\text{k}}) \cdot (gc_{\text{p}+1} - gc_{\text{p}}) }{ (li_{\text{k}+1} - li_{\text{k}})^{2} \cdot (sc_{\text{p}+1} - sc_{\text{p}}) } \\ \dfrac{ \partial c}{ \partial li_{\text{k}+1}} = \dfrac{ (li_{\text{k}} - li) \cdot (gi_{\text{k}+1} - gi_{\text{k}}) \cdot (gc_{\text{p}+1} - gc_{\text{p}}) }{ (li_{\text{k}+1} - li_{\text{k}})^{2} \cdot (sc_{\text{p}+1} - sc_{\text{p}}) } \\ \dfrac{ \partial c}{ \partial gc_{\text{p}}} = \dfrac{ (li_{\text{k}} - li) \cdot (gi_{\text{k}+1} - gi_{\text{k}}) + (gi_{\text{k}} - sc_{\text{p}}) \cdot (li_{\text{k}} - li_{\text{k}+1}) }{ (li_{\text{k}+1} - li_{\text{k}}) \cdot (sc_{\text{p}+1} - sc_{\text{p}}) } + 1 \\ \dfrac{ \partial c}{ \partial gc_{\text{p} + 1}} = \dfrac{ (li - li_{\text{k}}) \cdot (gi_{\text{k}+1} - gi_{\text{k}}) + (gi_{\text{k}} - sc_{\text{p}}) \cdot (li_{\text{k}+1} - li_{\text{k}}) }{ (li_{\text{k}+1} - li_{\text{k}}) \cdot (sc_{\text{p}+1} - sc_{\text{p}}) } \\ \dfrac{ \partial c}{ \partial sc_{\text{p}}} = \dfrac{ (li - li_{\text{k}}) \cdot (gi_{\text{k}+1} - gi_{\text{k}}) + (gi_{\text{k}} - sc_{\text{p}+1}) \cdot (li_{\text{k}+1} - li_{\text{k}}) }{ (li_{\text{k}+1} - li_{\text{k}}) \cdot (sc_{\text{p}+1} - sc_{\text{p}})^{2} } \cdot (gc_{\text{p}+1} - gc_{\text{p}}) \\ \dfrac{ \partial c}{ \partial sc_{\text{p}+1}} = \dfrac{ (li_{\text{k}} - li) \cdot (gi_{\text{k}+1} - gi_{\text{k}}) + (sc_{\text{p}} - gi_{\text{k}}) \cdot (li_{\text{k}+1} - li_{\text{k}}) }{ (li_{\text{k}+1} - li_{\text{k}}) \cdot (sc_{\text{p}+1} - sc_{\text{p}})^{2} } \cdot (gc_{\text{p}+1} - gc_{\text{p}}) \end{array}\) |
Les incertitudes sont contenues dans les tables d'étalonnage. L'incertitude u(li) sur la valeur li sera prise égale à zéro dans le calcul de la correction d'étalonnage. En effet, cette incertitude sera incluse par la suite dans le modèle de la mesure qui contiendra un terme de la forme « li + c ».
Remarque : dans cette évaluation de l'incertitudes, on ne prend pas en compte l'erreur commise en assimilant la courbe à une droite entre deux points d'étalonnage. Si les points d'étalonnage sont suffisamment proche, cette erreur est négligeable. Le lecteur souhaitant prendre en compte cette erreur pourra se reporter à [1] qui présente une méthode de calcul au moyen du théorème des accroissements finis.
La formule de calcul étant un peu lourde, celle-ci a été programmée sur le formulaire du paragraphe 3.
3. Formulaire de calcul en ligne
Le formulaire décompose le calcul en 5 étapes décrites dans le tableau 3.
| Etape | Titre | Action |
| 1 | Définition des unités | Il est ici demandé de saisir les unités de la grandeur appliquée à la sonde, de la grandeur affichée et du signal
transitant entre la sonde et l'afficheur.
La saisie effectuée, il faut valider, ce qui a pour effet de mettre à jour le formulaire avec les unités employées. |
| 2 | Indication de l'afficheur (en chaîne complète) | Saisir ici l'indication de la chaîne de mesure constituée de la sonde et de l'indicateur. Une fois la saisie effectuée, validez cette étape. |
| 3 | Données d'étalonnage de l'afficheur seul | Saisir les deux points d'étalonnage de l'afficheur qui encadrent la valeur indiqué par l'afficheur (qui a été
définie à l'étape 2).
La saisie effectuée, il faut valider, ce qui a pour effet de calculer la grandeur qui existe à l'entrée de l'afficheur (égale à la grandeur de sortie de la sonde). |
| 4 | Données d'étalonnage du capteur seul | Saisir les deux points d'étalonnage de la sonde qui encadrent la grandeur qui a été calculée à l'étape 3.
La saisie effectuée, il faut valider, ce qui a pour effet de calculer la grandeur qui est appliquée sur le capteur et d'afficher les résultats pour l'étape 5. |
| 5 | Résultats pour la chaîne complète | Relever la valeur de la correction pour la chaîne complète et l'incertitude sur cette correction. Pour exploiter ce résultat il est nécessaire de faire manuellement les arrondis. En règle générale, on garde deux chiffres significatifs pour l'incertitude. Concernant la correction, l'erreur commise par l'arrondi doit être inférieure à 10 % de l'incertitude. |
4.1. Table d'étalonnage de la chaîne complète
Soit une chaîne de température composée d'une sonde de température de type Pt100 et d'un indicateur. La sonde de température a été étalonnée en la plongeant dans un bain thermostatique dont on connaissait la température. Cet étalonnage a conduit à établir la relation entre la température appliquée sur la sonde et la résistance de cette sonde. Les résultats sont reproduits dans le tableau 4.
| Température de référence | Incertitude type sur la température | Résistance de la sonde (pour 1 mA) | Incertitude type sur la résistance |
| 0,000 °C | 0,004 °C | 100,013 6 Ω | 0,002 5 Ω |
| 20,041 °C | 0,007 °C | 107,832 4 Ω | 0,002 5 Ω |
| 28,238 °C | 0,007 °C | 111,016 5 Ω | 0,002 5 Ω |
| 36,337 °C | 0,007 °C | 114,154 1 Ω | 0,002 5 Ω |
| 44,894 °C | 0,007 °C | 117,460 8 Ω | 0,002 5 Ω |
L'indicateur a été étalonné par simulation : on a appliqué des résistances étalon aux bornes d'entrée et on a relevé la température donnée par l'afficheur. Cet étalonnage a conduit à établir la relation entre la résistance aux bornes de l'afficheur et la température affichée. Les résultats sont reproduits dans le tableau 5.
| Résistance de référence | Incertitude type sur la résistance | Température affichée | Incertitude type sur la valeur affichée |
| 68,327 Ω | 0,006 1 Ω | −80,00 °C | 0,016 °C |
| 99,999 Ω | 0,005 0 Ω | 0,00 °C | 0,016 °C |
| 138,504 Ω | 0,006 1 Ω | 100,00 °C | 0,016 °C |
| 175,853 Ω | 0,007 1 Ω | 200,00 °C | 0,016 °C |
Ce calcul a été effectué avec le formulaire de calcul en ligne (données par défaut lors du chargement du formulaire). On obtient avec un coefficient d'élargissement k = 2 :
| c = −0,384 °C ± 0,036 °C. |
Afin de valider le calcul développé, l'incertitude a également été calculée sur Gumy [2]. Le budget d'incertitudes calculé par ce logiciel est reproduit dans le tableau 6. Celui-ci montre au travers de la colonne « contribution » que les composantes liées à l'étalonnage du capteur et de l'indicateur participent à l'incertitude d'étalonnage de la chaîne complète. Cela prouve qu'il faut se méfier du raisonnement souvent utilisé qui consiste à dire que les composantes liées à l'afficheur son négligeables devant celles du capteur afin de ne pas faire de double interpolation.
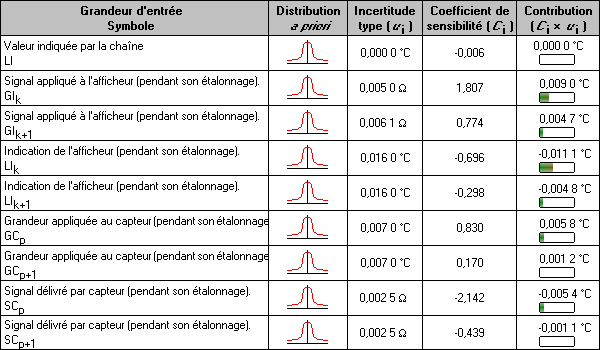
A partir du formulaire de calcul, la table d'étalonnage de la chaîne complète a été construite. Celle-ci est reproduite dans le tableau 7.
| Température affichée (L) |
Température de référence (T) |
Correction (c = T − L) |
Incertitude type sur la correction |
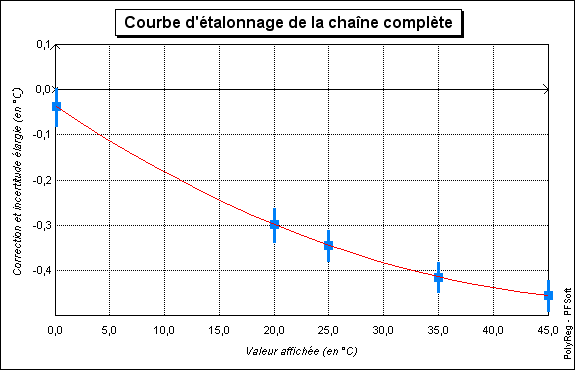
| 0,10°C | 0,0613 °C | −0,039 °C | 0,022 °C |
| 20,00 °C | 19,702 °C | −0,298 °C | 0,019 °C |
| 25,00 °C | 24,656 °C | −0,344 °C | 0,018 °C |
| 35,00 °C | 34,586 °C | −0,414 °C | 0,017 °C |
| 45,00 °C | 44,546 °C | −0,454 °C | 0,018 °C |
La courbe d'étalonnage correspondante, reproduite sur la figure 1, a été tracée à l'aide de PolyReg [3] :
Dans le cas ou l'entreprise choisi de ne pas appliquer des corrections d'étalonnage, mais de n'utiliser que des instruments vérifiés, la vérification devra être effectuée à partir de la table d'étalonnage reconstruite. Par exemple, si on se fixe une erreur maximale tolérée de ±0,5 °C avec la chaîne étudiée dans cet exemple, on produira une table de vérification telle que celle figurant dans le tableau 8.
| Température affichée (L) |
Valeur absolue de l'erreur (E = |L − T|) |
Incertitude élargie sur l'erreur (U) | Valeur à tester (E+U) | Spécification | Sanction |
| 0,10 °C | 0,039 °C | 0,044 °C | 0,083 °C | 0,5 °C | Conforme |
| 20,00 °C | 0,298 °C | 0,038 °C | 0,336 °C | 0,5 °C | Conforme |
| 25,00 °C | 0,344 °C | 0,036 °C | 0,380 °C | 0,5 °C | Conforme |
| 35,00 °C | 0,414 °C | 0,034 °C | 0,448 °C | 0,5 °C | Conforme |
| 45,00 °C | 0,454 °C | 0,036 °C | 0,490 °C | 0,5 °C | Conforme |
La chaîne est conforme à la spécification bien qu'en limite de tolérance à 45 °C.
Si on souhaite procéder à la vérification d'une chaîne de mesure dont les éléments ont été étalonnés séparément, cette méthode est la seule qui soit réaliste. Cette remarque n'est visiblement pas évidente puisque de nombreux industriels procèdent séparément à la vérification de leur capteurs et à la vérification de leurs afficheurs. En effet on peut avoir des éléments séparés qui sont hors spécifications, mais dont les erreurs se compensent et au final avoir une chaîne conforme. Inversement, et plus grave, on peut avoir deux éléments conformes en limite de spécifications dont les erreurs s'ajoutent dans un même sens et au final avoir une chaîne non conforme. Si l'on voulait éviter ce dernier problème, il faudrait alors réduire considérablement les spécifications de chaque élément, ce qui conduirait alors à déclarer non conforme, à tort, l'essentiel des instruments de mesure.
5. Validation du calcul d'incertitudes par la méthode de Monte-Carlo
L'évaluation de l'incertitude effectué en appliquant la loi de propagation des variances suppose que le modèle (1) est suffisamment linéaire. La méthode la plus simple, disponible à ce jour, pour vérifier que cette condition n'est pas contredite, est de comparer le résultat à un autre calcul d'incertitude utilisant la méthode de Monte-Carlo [4] à l'aide d'un outil tel que MC-Ed [5].
Le calcul effectué au moyen de MC-Ed [5] donne pour un échantillon de 1 million de valeurs, l'intervalle élargi à 95 % suivant :
| c ∈ [−0,419 °C ; −0,350 °C]. |
La statistique par classes obtenue avec MC-Ed représentant la moyenne et l'intervalle élargi à 95 % est représenté sur la figure 2.
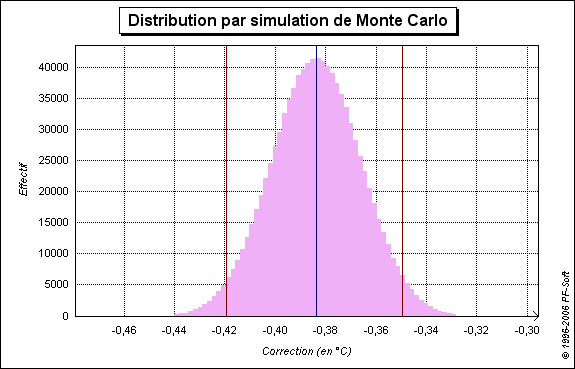
Les calculs effectués en utilisant la loi de propagation des variances et en utilisant la simulation de Monte-Carlo sont rappelés dans le tableau 9. Ceux-ci étant cohérents, l'application du GUM au modèle (1) n'est pas contredite.
| Propagation des variances (GUM) | Propagation des distributions (Monte-Carlo) |
| c = −0,384 °C Uk = 2 = 0,036 °C |
c = −0,384 °C c1 = −0,419 °C c2 = −0,350 °C |
| Ik = 2 = [−0,419 °C ; −0,349 °C] | I95 % = [−0,419 °C ; −0,350 °C] |
Le fichier contenant ce calcul, à utiliser avec MC-Ed [5], est disponible dans le lien suivant (décompresser l'archive dans le répertoire de MC-Ed) :
 |
Calcul de l'incertitude avec MC-Ed |
Remarque : les échantillons occupant un espace mémoire important, ceux-ci ne sont pas inclus dans l'archive. Vous devrez les générer sur votre machine.
6. Conclusion / mise en oeuvre de la méthode
Il est clair que ce tableau d'étalonnage reconstruit pour la chaîne complète n'est pas un étalonnage. Ceci étant, le calcul étant tellement lourd, il est clair que les opérateurs disposant de deux certificats d'étalonnage pour le capteur et l'indicateur ne calculeront pas sur le terrain l'incertitude due à la double interpolation pour chaque valeur mesurée. Il est donc conseillé que le service métrologie ou à défaut le service qualité de l'entreprise émette une table d'étalonnage pour la chaîne complète, à l'image de l'exemple du paragraphe 4, et diffuse cette table dans les dossiers d'utilisation des instruments de mesure qui sont mis à disposition des utilisateurs.
| [1] | PLATEL F., Incertitude due à l'interpolation sur une table de données numériques, MetGen, 2004. |
| [2] | PLATEL F., « Calcul d'incertitudes avec Gumy », MetGen, Dossier métrologie 4. |
| [3] | PLATEL F., « Détermination du polynôme des moindres carrés par une méthode algébrique », MetGen, Dossier métrologie 2. |
| [4] | JCGM, "Evaluation of measurement data - Supplement 1 to the "Guide to the expression of uncertainty in measurement" - Propagation of distributions using a Monte-Carlo method", BIPM, JCGM 101:2008, 2008, www.bipm.org. |
| [5] | PLATEL F., « Mise en pratique de la méthode de Monte-Carlo - Projet Monte-Carlo Editor (MC-Ed) », MetGen, Dossier métrologie 25. |