
Dans la pratique les instruments de mesure ne sont pas utilisés exactement aux valeurs de leurs points d'étalonnage. Il est donc nécessaire de construire une modélisation permettant de calculer la correction sur l'ensemble de la plage d'étalonnage. La formulation mathématique permettant de calculer cette correction est déterminée à partir des résultats d'étalonnage qui sont entachés d'incertitudes, et donc ces incertitudes se propagent dans la formulation mathématique. Comme l'a rappelé la déclaration commune entre le BIPM, l'OIML, ILAC et l'ISO du 9 novembre 2011, la traçabilité en métrologie ne repose pas seulement sur une suite de raccordements à des étalons de référence, mais aussi sur l'évaluation des incertitudes. En d'autres termes, modéliser des résultats d'étalonnage sans fournir d'incertitude sur la modélisation est une rupture de la traçabilité. En l'absence de méthodes et d'outils de calculs, les laboratoires et les industriels établissent souvent des modélisations et utilisent des formulations qui majorent l'incertitude (par exemple avec des courbes enveloppant les incertitudes des points d'étalonnage). Cette méthode est en désaccord avec le GUM qui recommande que l'incertitude soit réaliste. De plus majorer l'incertitude est souvent pénalisant financièrement, en particulier quand les résultats de mesure sont utilisés pour une prise de décision, ou une analyse de risque. En réponse, ce dossier présente une méthode de calcul pour modéliser des résultats d'étalonnage, et l'incertitude associée à la modélisation. La méthode est incluse dans un logiciel de calcul. Celui-ci dispose d'une ergonomie permettant une prise en main par le plus grand nombre. Grâce à ce logiciel, les utilisateurs pourront exploiter les résultats des étalonnages tout en conservant la traçabilité.
Typiquement l'étalonnage consiste à appliquer une série de valeurs \( x_1, \ldots, x_n \) d'une grandeur de référence \( X \) à un instrument de mesure et à relever les indications correspondantes \( y_1, \ldots, y_n \) de la grandeur \( Y \) mesurée par l'instrument. Une fonction \( F \) est alors choisie comme approximation de la relation entre \( X \) et \( Y \). Cette fonction est choisie soit : 1) par la théorie si une relation physique entre \( X \) et \( Y \) existe ; 2) à partir de la répartition des points (\( x_i \), \( y_i \)) représentés sur une courbe de dispersion s'il n y a pas de théorie permettant de relier \( X \) et \( Y \).
Cette fonction fait intervenir un ensemble de paramètres qui sera noté \( A \) par la suite, et s'exprime sous la forme :
| \( Y = F(X, A) + \epsilon \) , | (1) |
avec l'erreur \( \epsilon \) qui est une variable aléatoire suivant une loi normale de moyenne nulle. Dans la pratique ce terme est appelé « résidu ».
La relation mathématique ainsi définie — qui est une équation paramétrique — est appelée fonction d'étalonnage. Les coefficients \( A \) sont déterminés à partir des résultats d'étalonnage. Les valeurs \( x_1, \ldots, x_n \) et \( y_1, \ldots, y_n \) étant entachées d'incertitudes, la relation (1) n'est pas déterministe, dans le sens ou elle ne passe pas par tous les points d'étalonnage — même si elle est définie par la théorie —, mais stochastique, ce qui explique que généralement les coefficients sont calculés par une méthode de régression. Les différents paramètres de l'ensemble \( A \) sont déterminés à partir de ces valeurs et possèdent donc des incertitudes. De plus, les différents paramètres étant calculés à partir de valeurs communes (\( x_1, \ldots, x_n \) et \( y_1, \ldots, y_n \)), ceux-ci sont corrélés entre eux.
Remarque : dans certains cas, la fonction d'étalonnage est établie entre la grandeur de référence \( X \) et la correction \( X - Y \) ou l'erreur \( Y - X \). Pour simplifier les notations, le cas « \( Y = F(X, A) \) » sera toujours considéré dans ce dossier. Il suffira de remplacer « \( Y \) » par « \( X - Y \) » ou par « \( Y - X \) » dans les applications.
L'évaluation de l'incertitude sur une réalisation \( y \) de la variable aléatoire \( Y \) correspondant à une réalisation \( x \) de \( X \) par la relation (1) peut être faite en appliquant la loi de propagation des variances [1]. Par conséquent, il est nécessaire de connaître les incertitudes de \( x \), des paramètres \( A \) et les covariances entre les différents paramètres.
Dans le cas le plus général, les métrologues utilisent un polynôme comme fonction d'étalonnage. Le choix de la fonction d'étalonnage se résume alors à définir le degré \( d \) du polynôme. Le choix peut se faire par la théorie si une relation physique polynomiale existe entre les grandeurs \( X \) et \( Y \) ou par une méthode graphique en choisissant la courbe la plus « harmonieuse » [2]. Dans ce cas, l'objectif de l'étalonnage sera de déterminer les valeurs numériques des coefficients \( a_0, \ldots, a_\text{d} \) du polynôme.
Soient \( \mathcal{F} \) un ensemble de fonctions et \( \mathcal{l} \) une fonction qui sera appelée fonction de coût. En conservant les notations précédentes pour les grandeurs \( X \) et \( Y \), la régression consiste à trouver une fonction \( f \) de \( \mathcal{F} \) minimisant la grandeur :
| \( \begin{eqnarray}D = \sum_{\text{i} = 1}^{\text{n}} \mathcal{l}\left(y_{\text{i}} - f(x_{\text{i}})\right)\end{eqnarray} \) . | (2) |
Ce qui s'écrit en utilisant l'argument minimum :
| \( \begin{eqnarray} D = \underset{ f\;\in\;\mathcal{F} }{\text{arg min}} \sum_{\text{i} = 1}^{\text{n}} \mathcal{l}\left(y_{\text{i}} - f(x_{\text{i}})\right) \end{eqnarray} \) . | (3) |
Cette expression n'a de sens que s'il y a unicité de la fonction \( f \) pour laquelle la fonction \( \mathcal{l} \) est minimalisée. Dans la pratique cette condition n'est pas vérifiée ne serait-ce que parce qu'il existe une infinité de fonctions pour lesquelles \( y_{\text{i}} = f(x_{\text{i}}), i \in \{1, \ldots, n\} \). En restreignant \( \mathcal{F} \) à un type de fonction (par exemple les polynômes d'un certain degré) la condition peut être vérifiée [2].
Concernant la fonction de coût, l'usage se limite à deux fonctions :
- le coût absolu \( \mathcal{l}(u) = |u| \) ;
- le coût quadratique \( \mathcal{l}(u) = u^2 \).
Dans la pratique, seul le coût quadratique est utilisé. On parle alors de calcul par les moindres carrés.
Cette méthode dite de régression par les moindres carrés est généralement utilisée pour modéliser les résultats d'étalonnage. Concernant les évaluations d'incertitudes, il existe des formules obtenues par calculs sur les variances mais qui nécessitent de nombreuses hypothèses simplificatrices (pas d'incertitudes sur les valeurs \( x_{\text{i}} \), incertitudes sur les valeurs \( y_{\text{i}} \) toutes égales) [3] qui ne correspondent pas à la réalité. Ce problème peut être résolu en couplant la méthode de régression avec la méthode de Monte-Carlo.
3. Couplage de la régression avec la méthode de Monte-Carlo
La méthode de Monte-Carlo a été inventée au milieu du 20e siècle et désigne toute méthode permettant de calculer une valeur numérique au moyen de simulateurs de nombres aléatoires. Dans la pratique les nombres aléatoires générés ne sont pas véritablement aléatoires car ils correspondent à une séquence prédéterminée : on parle de générateurs pseudo-aléatoires. Typiquement la méthode de Monte-Carlo est utilisée pour évaluer des intégrales [4]. L'intérêt de cette méthode est également de pouvoir fournir un résultat sous la forme d'un échantillon, ce qui ouvre la voie à divers calculs statistiques.
C'est cette dernière particularité qui a été exploitée dans le cadre du Supplément 1 du GUM [5] pour déterminer une distribution de la grandeur dont on veut déterminer l'incertitude de mesure. Cette méthode a permis de s'affranchir des hypothèses de linéarité des modèles de la mesure faites dans la méthode de propagation des variances du GUM [1]. Depuis la sortie du Supplément 1 du GUM de nombreuses publications dans des revues à comité de lecture sur l'application de cette méthode en métrologie ont confirmé sa robustesse. Quelques logiciels généralistes en mathématiques permettent d'appliquer cette méthode, et plus spécifiquement en métrologie, le logiciel MC-Ed [6] a été élaboré spécifiquement pour l'évaluation des incertitudes de mesure.
3.2. Application à la régression polynomiale
Dans le cas présent, il s'agit d'une variante de la méthode recommandée par le GUM puisqu'elle ne sera pas appliquée sur un modèle de la mesure mais pour générer une suite de polynômes et déterminer ainsi des distributions des différents coefficients.
En conservant les notations précédentes, la méthode consiste à générer dans un premier temps des échantillons pour chaque doublet \( (X_{\text{i}}, Y_{\text{i}}) \). En d'autres termes il est nécessaire de connaître les incertitudes \( (u_{\text{xi}}, u_{\text{yi}}) \) et de définir les lois de probabilité \( (d_{\text{xi}}, d_{\text{yi}}) \) de chaque doublet \( (X_{\text{i}}, Y_{\text{i}}) \). Dans la pratique les incertitudes sur les \( Y_{\text{i}} \) sont connues puisqu'il s'agit des incertitudes d'étalonnage et dans ce cas la loi normale présente l'entropie maximale. La question des \( X_{\text{i}} \) est plus problématique. En l'absence d'information il est possible, faute de mieux, d'évaluer une incertitude à partir d'une mesure de répétabilité et de la résolution de l'appareil.
Si \( m \) est la taille des échantillons et \( d \) le degré du polynôme recherché, il est possible de calculer une suite de \( m \) polynômes comme indiqué sur la figure 1. Cette suite de polynômes permet de déduire des échantillons de \( m \) valeurs pour chaque coefficient \( a_{0}, \ldots, a_{\text{d}} \) de la fonction d'étalonnage. A partir de ces derniers échantillons, il est possible de calculer une moyenne et un écart type pour chaque coefficient, et de calculer des covariances entre chaque coefficient.

Dans cette méthode de calcul, un point mérite cependant l'attention du lecteur. Peut-on prendre la moyenne des coefficients des polynômes obtenus au moyen de simulations de Monte-Carlo pour définir un nouveau polynôme de modélisation ? La réponse est l'affirmative. Démontrons ce point.
En conservant les notations précédentes, soient \( x \in [x_{1} ; x_{\text{n}}] \) et \( y \) la « valeur vraie » correspondante. Par définition des polynômes de régression on a le système d'équations suivant :
| \( \left\{ \begin{array}{c} a_{0,1} & + & a_{1,1} \cdot x & + & \ldots & + & a_{\text{d},1} \cdot x^{\text{d}} & + & \epsilon_{1}(x) & = & y \\ . & & . & & & & . & & . & & . \\ . & & . & & & & . & & . & & . \\ . & & . & & & & . & & . & & . \\ a_{0,\text{m}} & + & a_{1,\text{m}} \cdot x & + & \ldots & + & a_{\text{d},\text{m}} \cdot x^{\text{d}} & + & \epsilon_{\text{m}}(x) & = & y \end{array} \right. \) . | (4) |
avec \( \epsilon_{\text{i}}(x) \) le résidu du \( i^{\text{e}} \) polynôme de régression au point \( x \).
En sommant les \( m \) équations de (4) et en les divisant par \( m \), on obtient le polynôme (5) :
| \( \begin{eqnarray} \sum_{\text{i} = 1}^{\text{m}} \frac{a_{0,\text{i}}}{m} + \left(\sum_{\text{i} = 1}^{\text{m}} \frac{a_{1,\text{i}}}{m}\right) \cdot x + \ldots + \left(\sum_{\text{i} = 1}^{\text{m}} \frac{a_{\text{d},\text{i}}}{m}\right) \cdot x^{d} + \sum_{\text{i} = 1}^{\text{m}} \frac{\epsilon_{\text{i}}(x)}{m} = y \end{eqnarray} \) | (5) |
Dans ce polynôme les coefficients sont les moyennes des coefficients des polynômes obtenus par simulations de Monte-Carlo.
On appelle \( \epsilon_{\text{mod}}(x) \) la moyenne des résidus des différentes modélisations au point \( x \), \( \epsilon_{\text{min}}(x) \) et \( \epsilon_{\text{max}}(x) \) les valeurs minimum et maximum des résidus en \( x \) des différents polynômes de régresssion :
| \( \begin{eqnarray} \epsilon_{\text{mod}} (x) = \sum_{\text{i} = 1}^{\text{n}} \frac{\epsilon_{\text{i}}(x)}{m} \end{eqnarray} \) , | (6) | ||
| \( \begin{eqnarray} \epsilon_{\text{max}} (x) = \underset{ 1 \leqslant \text{i} \leqslant \text{m} }{\text{Max}} \epsilon_{\text{i}}(x) \end{eqnarray} \) , | |||
| \( \begin{eqnarray} \epsilon_{\text{min}} (x) = \underset{ 1 \leqslant \text{i} \leqslant \text{m} }{\text{min}} \epsilon_{\text{i}}(x) \end{eqnarray} \) , |
il vient alors :
| \( \epsilon_{\text{min}} (x) \leqslant \epsilon_{\text{mod}} (x) \leqslant \epsilon_{\text{max}} (x) \) . | (7) |
En d'autres termes le résidu \( \epsilon_{\text{mod}} (x) \) du polynôme dont les coefficients sont définis par la moyenne des coefficients des polynômes de régression a l'ordre de grandeur d'un résidu de modélisation obtenu par la méthode des moindres carrés, ce qui démontre que pour un usage métrologique ce polynôme est une modélisation pertinente.
Cette méthode est très robuste en raison de sa simplicité. Ceci étant, elle est très lourde à mettre en oeuvre et nécessite de ce fait un logiciel spécifique. La contrepartie de la robustesse de cette méthode est que les temps de calcul peuvent être élevés. Par exemple le calcul sur un polynôme du 3e degré avec le logiciel MC-Reg (présenté dans la suite de ce dossier) peut atteindre une trentaine de minutes avec un PC de bureau ordinaire. Toutefois ce temps de calcul doit être mis en balance avec sa périodicité et son apport : en général il sera effectué une fois par an lors de l'étalonnage de l'instrument de mesure et permettra d'exploiter réellement l'étalonnage. D'autre part lorsque les calculs sont en cours, le logiciel MC-Reg ne nécessite pas la présence d'un opérateur. En d'autre terme, les calculs peuvent être fait en temps masqué.
Soit \( k \in \{1 ; n\} \) et \( p \in P[X] \) le polynôme d'étalonnage. D'après la relation (1), le \( k^{\text{e}} \) résidu vaut :
| \( \epsilon_{\text{k}} = y_{\text{k}} - p(x_{\text{k}}) \) . | (8) |
La statistique :
| \( \begin{eqnarray} \sigma_{\epsilon}^{2} = \sum_{\text{p} = 1}^{\text{n}} \frac{\epsilon_{\text{p}}^{2}}{n - 2} \end{eqnarray} \) , | (9) |
est un estimateur sans biais de \( \epsilon \) [7]. Toutefois, les incertitudes de modélisation calculées en prenant en compte cette valeur sont significativement inférieures aux incertitudes des points d'étalonnage (figure 2). La raison principale de cette sous-évaluation provient du fait qu'elle ne prends pas en compte l'incertitude sur les valeurs des « \( y_{\text{i}} \) », mais uniquement une valeur moyenne. Pour cette raison une méthode alternative basée sur des simulations de Monte-Carlo a été développé.

Soit \( i \in \{1 ; m\} \) et \( j \in \{1 ; n\} \). En reprenant les notations de la figure 1, on appelle \( p_{\text{i}} \) le polynôme obtenu à la ie simulation. On définit l'erreur de modélisation obtenue lors de la ie simulation sur le je point d'étalonnage par :
| \( \epsilon_{\text{i},\text{j}} = p_{\text{i}}(x_{\text{i},\text{j}}) - y_{\text{i},\text{j}} \) . | (10) |
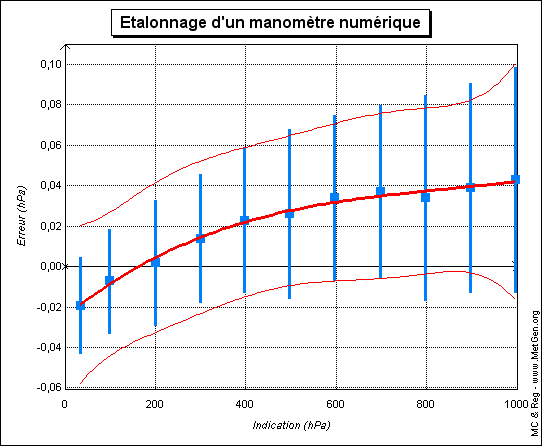
La moyenne et l'écart type de \( \epsilon \) seront alors évalués à partir de l'échantillon \( E = \{\epsilon_{\text{i},\text{j}}, i \in \{1 ; m\}~~\text{et}~~i \in \{1 ; n\}\} \) de \( m \cdot n \) valeurs. Dans la pratique, la moyenne de \( \epsilon \) est considérée comme nulle. L'incertitude type de \( \epsilon \) est prise égale à son écart type. L'écart type ainsi évalué conduit à des incertitudes de modélisation en accord avec les données d'étalonnage (figure 3).
4. Incertitude d’une valeur calculée avec un polynôme d’étalonnage
Soit le polynôme d'étalonnage \( p \in P[X] \) noté :
| \( p (x) = a_{0} + a_{1} \cdot x + a_{2} \cdot x^{2} + \ldots + a_{\text{d}} \cdot x^{\text{d}} \) . | (11) |
avec : \( x \in \mathbb{R} \) et \( (a_{0}, \ldots, a_{\text{d}}) \in \mathbb{R}^{\text{d} + 1} \).
Le « modèle de la mesure » s'écrit :
| \( y = p(x) + \epsilon \) . | (12) |
L'application de la loi de propagation des variances à (12) permet de calculer l'incertitude sur la valeur \( y \) en supposant que \( x \) et \( \epsilon \) ne sont pas corrélés avec les variables \( a_{0}, \ldots, a_{\text{d}} \) par la relation :
| \( \begin{eqnarray}u(y) = \sqrt{ u^{2}(x) \cdot p_{1}^{2}(x) + \sum_{\text{i} = 0}^{\text{d}} u^{2}(a_{\text{i}}) \cdot x^{2 \times \text{i}} + 2 \times \sum_{\text{i} = 0}^{\text{d} - 1} \sum_{\text{j} = \text{i} + 1}^{\text{d}} x^{\text{i}+\text{j}} \cdot \text{cov}~(a_{\text{i}}, a_{\text{j}}) + u^{2}(\epsilon)} \end{eqnarray} \) | (13) |
avec : \( p_{1}(x) = a_{1} + 2 \times a_{2} \cdot x + \ldots + i \cdot a_{\text{i}} \cdot x^{\text{i}-1} + \ldots + d \cdot a_{\text{d}} \cdot x^{\text{d}-1} \), \( i \in \{1, \ldots, d\} \).
5. Le logiciel Monte-Carlo & Regression (MC-Reg)
Le logiciel MC-Reg utilise le Pack Monte-Carlo [8] qui est en particulier utilisé par le logiciel de calcul d'incertitudes MC-Ed [6].






| |
|
Le logiciel MC-Reg est fourni en version portable. Celui-ci effectuant de très nombreux accès au disque pour écrire et lire les échantillons de valeurs, il est conseillé de l'installer sur un disque dur externe de travail (par exemple connecté via le port USB) afin de ménager le disque de votre ordinateur.
Exemples de rapports de calcul générés par MC-Reg
Les exemples ci-dessous sont des rapports au format pdf générés automatiquement par MC-Reg. Ces rapports peuvent être imprimés et ainsi archivés dans le cadre d'un système qualité.
| N° | Titre | |
| 1 |  |
étalonnage d'un thermomètre doté d'une sonde à résistance de platine Pt100 |
| 2 |  |
étalonnage d'un manomètre numérique |
| 3 |  |
étalonnage d'une chaîne de température (annexe H du GUM) |
| 4 |  |
étalonnage d'une chaîne de température – Polynôme du troisième degré |
Le fichiers de calcul de ces exemples sont fournis avec le logiciel MC-Reg.
6.1. Étalonnage d'une chaîne de température – Droite des moindres carrés
Cet exemple est extrait de l'annexe H du GUM [1]. Le tableau 1 reproduit les données d'étalonnage.
| Valeur indiquée t (°C) |
t − 20 °C | Correction (°C) |
Incertitude type sur la correction (°C) |
| 21,521 | 1,521 | −0,171 | 0,003 5 |
| 22,012 | 2,012 | −0,169 | 0,003 5 |
| 22,512 | 2,512 | −0,166 | 0,003 5 |
| 23,003 | 3,003 | −0,159 | 0,003 5 |
| 23,507 | 3,507 | −0,164 | 0,003 5 |
| 23,999 | 3,999 | −0,165 | 0,003 5 |
| 24,513 | 4,513 | −0,156 | 0,003 5 |
| 25,002 | 5,002 | −0,157 | 0,003 5 |
| 25,503 | 5,503 | −0,159 | 0,003 5 |
| 26,010 | 6,010 | −0,161 | 0,003 5 |
| 26,511 | 6,511 | −0,160 | 0,003 5 |
Le GUM précise que l'incertitude de l'indication du thermomètre est négligeable et utilise comme variable d'entrée (t − 20 °C). La modélisation sera donc de la forme :
| \( y = a_{0} + a_{1} \cdot (t - 20 \text{°C}) + \epsilon \) . | (14) |
Les résultats de MC-Reg et du GUM [1] sont reproduits dans le tableau 2.
| Grandeur | GUM | MC-Reg |
| a0 | −0,171 2 °C | −0,171 2 °C |
| a1 | 0,002 18 | 0,002 18 |
| u (a0) | 0,002 9 °C | 0,002 9 °C |
| u (a1) | 0,000 67 | 0,000 67 |
| r (a0 ; a1) | −0,930 | −0,930 |
Ce tableau montre que le calcul effectué par MC-Reg sur une droite de régression est en accord avec le GUM [1]. La modélisation des résultats d'étalonnage effectuée par MC-Reg est reproduite sur la figure 5.

Pour des polynômes de degré supérieur et avec des incertitudes différentes sur les données d'entrée, il n'a pas été possible de comparer les calculs faute de méthode disponible dans les publications. On peut toutefois s'assurer graphiquement que le calcul effectué par MC-Reg ne conduit pas à une incohérence avec les incertitudes des points d'étalonnage comme dans l'exemple suivant.
6.2. étalonnage d'une chaîne de température – Polynôme du troisième degré
Le tableau 3 extrait de [2] reproduit la table d'étalonnage d'une chaîne de température dotée d'un thermocouple de type K.
| Valeur étalon (°C) |
Valeur appareil (°C) |
Erreur (°C) |
Incertitude élargie sur l'erreur (°C) |
| 0,00 | −0,5 | −0,5 | 0,5 |
| 149,47 | 150,2 | 0,7 | 1,0 |
| 298,80 | 297,5 | −1,3 | 1,5 |
| 500,40 | 499,9 | −0,5 | 2,0 |
| 700,00 | 698,9 | −1,1 | 2,0 |
| 899,80 | 897,3 | −2,5 | 3,0 |
| 1 099,50 | 1 095,0 | −4,5 | 4,0 |
Dans le cas présent la fonction d'étalonnage devra permettre de calculer l'erreur pour une indication de l'appareil. La première étape consiste à trouver le degré du polynôme le mieux approprié à ces données. La méthode et le logiciel PolyReg à employer sont fournis dans [2]. L'utilisation du logiciel PolyReg sur les données du tableau 4 conduit à retenir un polynôme du troisième degré.
| Valeur Appareil (°C) |
Erreur (°C) |
Incertitude élargie sur l'erreur (°C) |
Pondération |
| −0,5 | −0,5 | 0,5 | 0,65 |
| 150,2 | 0,7 | 1,0 | 0,16 |
| 297,5 | −1,3 | 1,5 | 0,07 |
| 499,9 | −0,5 | 2,0 | 0,04 |
| 698,9 | −1,1 | 2,0 | 0,04 |
| 897,3 | −2,5 | 3,0 | 0,02 |
| 1 095,0 | −4,5 | 4,0 | 0,01 |
Ensuite, le calcul effectué avec MC-Reg en utilisant des échantillons de 106 valeurs conduit aux résultats reproduits dans le tableau 5.
| Grandeur | Valeur calculée par MC-Reg |
| a0 | −0,44 °C |
| a1 | 0,004 5 |
| a2 | −1,1×10−5 °C−1 |
| a3 | 4,0×10−9 °C−2 |
| u (a0) | 0,25 °C |
| u (a1) | 0,004 6 |
| u (a2) | 1,4×10−5 °C−1 |
| u (a3) | 9,8×10−9 °C−2 |
| cov (a1 ; a0) | −0,000 46 °C |
| cov (a2 ; a0) | 8,8×10−7 |
| cov (a2 ; a1) | −5,8×10−8 °C−1 |
| cov (a3 ; a0) | −4,8×10−10 °C−1 |
| cov (a3 ; a1) | 3,8×10−11 °C−2 |
| cov (a3 ; a2) | −1,3×10−13 °C−3 |
| ε | 0,07 °C |
| u (ε) | 0,95 °C |
La représentation graphique des résultats d'étalonnage, la modélisation correspondante et l'incertitude associée sont représentées sur la figure 6.

7. Exploitation des courbes d'étalonnage
Après avoir fait une modélisation des résultats d'étalonnage, il est intéressant de confronter la courbe d'étalonnage (valeur moyenne et enveloppe de l'incertitude) avec les données d'étalonnage initiales, ce que propose le logiciel MC-Reg. On observe généralement une élévation de l'incertitude aux points d'étalonnage ou l'incertitude était initialement plus faible. Par exemple sur la figure 3, la valeur de l'incertitude type sur la valeur modélisée correspondant au premier point d'étalonnage est 0,020 hPa contre 0,012 hPa pour le point d'étalonnage correspondant. La raison de cet écart provient du fait que la modélisation exploite l'ensemble des données d'étalonnage. Cela conduit à augmenter certaines incertitudes, mais conduit également à renforcer la confiance dans l'étalonnage en exploitant la cohérence entre l'ensemble des données de l'étalonnage. En effet, lorsqu'il est acquis que les résultats d'étalonnage respectent une forme de fonction donnée, la modélisation prend tout son intérêt lorsqu'un point sort de l'enveloppe de l'incertitude. C'est par exemple le cas du 3e point d'étalonnage de la figure 6. Dans ce cas, il faut s'interroger sur la pertinence de ce point d'étalonnage, et idéalement refaire la mesure. En résumé la modélisation amène à examiner avec un oeil critique les résultats d'étalonnage, ce qui est aussi le rôle du métrologue.
8. Autres méthodes et perspectives
La nouvelle définition de l'étalonnage suite à la troisième édition du VIM
[9]
a entraîné la mise en place de programmes d'études pour modéliser les résultats d'étalonnage.
Formellement la nouvelle définition de l'étalonnage ne requiert pas de modéliser les résultats d'étalonnage
[10].
Ceci étant cette opération est souvent nécessaire pour exploiter ces résultats. Il y a peu de publications à
comité de lecture sur le sujet, les seuls éléments disponibles au moment de la rédaction de ce dossier
(milieu de l'année 2012) sont des communications faites dans le cadre de séminaires ou de congrès. Les travaux menés
reposent essentiellement sur la méthode des moindres carrés généralisés. Il faut toutefois prendre garde à
certaines méthodes qui peuvent conduire à sous-estimer les incertitudes contrairement à la méthode de Monte-Carlo.
Les exemples de courbes d'étalonnage contenues dans ce dossier montrent d'ailleurs que les incertitudes obtenues sont cohérentes
avec les données d'étalonnage, et que des incertitudes plus faibles ne seraient plus en accord avec ces données.
Le logiciel MC-Reg met en oeuvre une technique de régression avec des polynômes. Ceci étant la méthode
générale peut s'appliquer à tout autre type de fonction. De plus la programmation de MC-Reg reposant sur des modules
fonctionnant en ligne de commande, il est possible d'adapter le logiciel pour d'autres fonctions.
Un autre aspect à traiter concerne la validation de la méthode et du logiciel. Les calculs ont été comparés
aux calculs effectués pour la droite des moindres carrés qui ont été publiés dans le GUM
[1].
Pour les polynômes de degré au moins égal à 2 ,en l'absence d'autres méthodes, la seule solution
possible aujourd'hui est de comparer les résultats au logiciel réalisé par le NPL
[11]
et diffusé par le BIPM
[12].
Ceci étant ce logiciel ne permet de traiter que les polynômes dont le degré est inférieur à 4,
et il n'a pas été possible de le faire fonctionner avec d'autres données que l'exemple d'utilisation
contenu dans sa documentation (qui concerne la droite des moindres carrés). Le manque
de méthodes et d'outils est particulièrement surprenant car la modélisation des résultats des étalonnages est indispensable
pour pouvoir les exploiter, en somme pour simplement maîtriser les mesures faites dans les entreprises et les laboratoires.
| [1] | JCGM, « évaluation des données de mesure - Guide pour l'expression de l'incertitude de mesure », BIPM, JCGM 100:2008 (version française), septembre 2008, www.bipm.org. |
| [2] | PLATEL F., « Détermination du polynôme des moindres carrés par une méthode algébrique », MetGen, Dossier métrologie 2. |
| [3] | PLATEL F., « Droite des moindres carrés et incertitude », MetGen, Dossier métrologie 14. |
| [4] | MONAHAN J.F., "Numerical Methods of Statistics", Cambridge University Press, 2001. |
| [5] | JCGM, "Evaluation of measurement data - Supplement 1 to the "Guide to the expression of uncertainty in measurement" - Propagation of distributions using a Monte-Carlo method", BIPM, JCGM 101:2008, 2008, www.bipm.org. |
| [6] | PLATEL F., « Mise en pratique de la méthode de Monte-Carlo - Projet Monte-Carlo Editor (MC-Ed) », MetGen, Dossier métrologie 25. |
| [7] | CORNILLION P.-A. et MATZNER-LOBER E., « Régression avec R », Springer, 2011. |
| [8] | PLATEL F., « Outils complémentaires pour la méthode de Monte-Carlo. Le "Pack Monte-Carlo". », MetGen, Dossier métrologie 24. |
| [9] | JCGM, « Vocabulaire international de métrologie - Concepts fondamentaux et généraux et termes associés (VIM) », BIPM, JCGM 200:2008 (E/F), www.bipm.org. |
| [10] | PLATEL F., « Lexique, Modification de la définition du terme étalonnage », MetGen. |
| [11] | NPL, "XGENLINE (8.1)", http://www.npl.co.uk/.../software-downloads-(ssfm). |
| [12] | BIPM, "Software for Measurement Uncertainty Evaluation", www.bipm.org/en/publications/guides/gum.html. |